すくい角，切削比，せん断角

切りくず厚さを測定し，切込み深さや工具のすくい角の情報と組み合わせると，せん断角を計算することができます．
なんとなく，すくい角の情報は不要だと思っていたのですが，切りくずの流出方向を決めることになるため，すくい角も必要らしいです．
ここでは，そのせん断角を計算するための関係式を導出する過程を確認します．
ただし，せん断角を仮想平面としてとらえた場合の話なので，厳密にはせん断面は平面ではないことには注意が必要です．



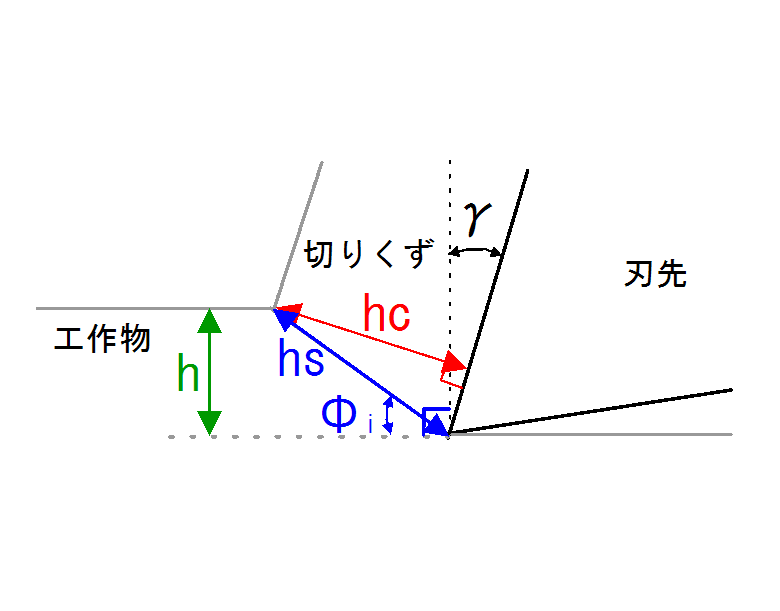
\( \phi_{i} \): せん断角
\( \gamma \): すくい角
\( h \): 切込み深さ（切り取り厚さ）
\( h_{s} \): せん断面の長さ
\( h_{c} \): 切りくず厚さ

上図において，次式を用いることでせん断角を求めることができます．

\( \phi_{i} = \tan^{-1} \lbrace \cfrac{C_{h}\cos( \gamma ) }{ 1 - C_{h}\sin( \gamma ) } \rbrace \)

\( C_{h} = \cfrac{h}{h_{c}} \): 切削比
＊通常，\( 0 < h \)かつ\( h < h_{c} \)であるため，\( 0 < C_{h} < 1 \)となります．

以下に，上式を導出する手順について示します．
まず，切込み深さ\( h \)とせん断面の長さ\( h_{s} \)の関係は次式で表されます．

\( \cfrac{h}{h_{s}}= \sin(\phi_{i}) \)
より，
\( h_{s}= \cfrac{h}{\sin(\phi_{i})} \)
が得られます．

次に，切りくず厚さ\( h_{c} \)とせん断面の長さ\( h_{s} \)の関係を導出します．
せん断面を抜けた材料は，すくい面に沿って平行に流出します．
このことから次式が成立します．

\( \cfrac{h_{c}}{h_{s}}= \cos(\phi_{i} - \gamma) \)

ここで次式の関係を用いると

\( \cos(A-B)=\cos(A)\cos(B)+\sin(A)\sin(B) \)

次式に変形できます．

\( \cfrac{h_{c}}{h_{s}}= \cos(\phi_{i})\cos(\gamma) + \sin(\phi_{i})\sin(\gamma) \)

ここに切込み深さ\( h \)とせん断面の長さ\( h_{s} \)の関係式を代入します．

\( \cfrac{h_{c}}{h}\sin(\phi_{i})= \cos(\phi_{i})\cos(\gamma) + \sin(\phi_{i})\sin(\gamma) \)
\( \cfrac{h_{c}}{h}\tan(\phi_{i})= \cos(\gamma) + \tan(\phi_{i})\sin(\gamma) \)
\( \tan(\phi_{i})= \cfrac{h}{h_{c}}\cos(\gamma) + \cfrac{h}{h_{c}}\tan(\phi_{i})\sin(\gamma) \)
\( \lbrace 1 - \cfrac{h}{h_{c}}\sin(\gamma) \rbrace \tan(\phi_{i})= \cfrac{h}{h_{c}}\cos(\gamma) \)
\( \lbrace 1 - C_{h}\sin(\gamma) \rbrace \tan(\phi_{i})= C_{h}\cos(\gamma) \)
\( \tan(\phi_{i})= \cfrac{ C_{h}\cos(\gamma) }{ 1 - C_{h}\sin(\gamma) } \)
\( \phi_{i}= \tan^{-1} \lbrace \cfrac{ C_{h}\cos(\gamma) }{ 1 - C_{h}\sin(\gamma) } \rbrace \)

よって，すくい角\( \gamma \)と切削比\( C_{h} \)からせん断角\( \phi_{i} \)を求める式が導出できました．

それでは，すくい角は工具形状から決まるとして，切削比が簡単にわかるかというとそうでもないです．
それは切りくずの厚みの測定が必要だからです．

切りくずの厚みは，加工開始直後，加工途中，加工終了直前で変化しています．
また，切りくずの自由面側の形状が波打っている場合があり，その場合は測定が難しくなります．
金属の体積自体は変化しないとすると，切りくずの長さから厚みが逆算できる場合があります．
切り屑の長さから厚みを逆算すると，切りくず厚みの平均値を求めることができます．
しかしながら，切りくずの横流れが発生していると，切りくずが幅方向にも変化しているため，体積からの逆算はできなくなります．

参考文献：
精密工学講座　切削工学，コロナ社，p290
中山一雄，機械工学大系36　切削加工論，コロナ社，p17