切りくずの細分化方法
切削時に発生する切りくずは,ある程度の長さにして,処理しやすくする必要があります.
これは,切りくずが長くなると,切削工具や工作物に絡みついて,加工の継続が困難になったり,工作物に傷がつく場合があるためです.
また,切りくずが大きな塊を形成すると,チップコンベアで運ぶことも難しくなります.
では,切りくずの長さを制御するには,どういった方法があるでしょうか.
それを以下に示します.
- 切削加工を断続にする
切削工具と工作物を加工途中に離してエアカット状態を作り,切りくずの連続性を強制的に失わせることで,切りくずの長さを制御します.
- 連続加工である旋削加工を,断続加工である転削加工に変更する
加工法そのものを変えるので,適用できない場合も多い.
旋削加工をミルターニングに変えるようなイメージ.
- プリグルーブ切削にする
工作物に溝を事前に切っておくことで,そこを切削工具が通過するときに,エアカットになり,切りくずが短くなる.
- 揺動切削やステップ加工にする
工具を工作物から一瞬離すことでエアカット状態を作り,切りくずを短くする.
- 連続加工である旋削加工を,断続加工である転削加工に変更する
- 外力を加える
切りくずに荷重を加えて破断させることで,切りくずの長さを制御します.
- 切りくずの成長先で逃げ面や邪魔板と接触させて,その反力で破断させる
一般的な切りくず処理のイメージ.
接触によって荷重を加えるため,荷重と変位の制約があり,なかなか難しい.
- 切削油剤やエアを切りくずに当てて,その荷重で破断させる
積極的に外力を加える方法で,高圧クーラントだと実施しやすい.
- 切りくずを長くして重力による荷重で破断させる
切りくずが細い場合は,これで切れることもある.
- チップブレーカ上で荷重をかけて破断させる
すくい面上に大きな段差を研削加工で設けておいて,そこに切りくずを当てて,破断させる.
結構無理がある.
- 切りくずの成長先で逃げ面や邪魔板と接触させて,その反力で破断させる
しかしながら,旋削加工を転削加工に変えるのは,そもそも無理な場合がほとんどです.
また,プリグルーブ切削や揺動切削では,切込み量が一定にならない,という問題があり,加工面性状が一定にならない可能性があります.
「外力を加える」方法のほうが一般的だと思います.
切りくずが成長して,切削工具の逃げ面とかホルダに接触して,破断する場合が理想形で,切削工具メーカもそれを狙っているのだと思います.
そうならない場合が,めんどくさいです.
色々調整して,切りくずを破断させる方法を探るわけですが,切りくずの幅や厚み,被削材,つまり,加工条件によっては,そもそも切りくずが外力によって折れない場合があります.
これは,どうやっても折れない切りくずがある,という意味です.
そこらへんのことは「チップブレーカの研究」に記載があります.
簡単に言えば「切りくずをバッカンから拾って,曲率を大きくするほうに手で曲げて真っすぐにしてみたときに,切りくずが破断しないなら,その切りくずは何をしても破断しない」ということです.
その状態にある切りくずは,どこに当てたりしても折れないので,邪魔板の位置を変えたりしても,切りくずを破断させるのは難しいです.
ただし,厳密には,加工中の切りくずと,加工後の切りくずには違いがあります.
それは,切りくず自体の温度と,切削点とつながっているかどうか,の2つです.
切りくずの端部に荷重を加えて,モーメントを発生させた場合,切削点には大きな荷重がかかり,かつ,切削点は高温になっているために,材料強度が下がっています.
よって,加工後の切りくずが破断できなくても,上記状態であれば,切りくずの破断ができるのかもしれません.
ですので,あくまでも目安として知っておくとよいと思います.
ここからは,切りくずの破断条件について考えてみます.
切りくずの成長先で逃げ面や邪魔板と接触させて,その反力で破断させる場合の破断条件について「チップブレーカの研究」に記載があります.
\( \varepsilon = \cfrac{ t_{2} }{2}( \cfrac{ 1 }{ R_{0} } - \cfrac{ 1 }{ R_{L} } ) \)
\( \varepsilon \): 切りくずに生じるひずみ
\( t_{2} \): 切りくずの厚さ
\( R_{0} \): チップブレーカによって与えられた切りくずの半径
\( R_{L} \): 逃げ面などとの接触によって変形した後の切りくずの半径
この\( \varepsilon \)が破断ひずみ\( \varepsilon_{B} \)を超えると破断するため,\( R_{L} \)を大きくしていく過程のどこかで次式が満たされることになります.
\( \varepsilon_{B} \leq \cfrac{ t_{2} }{2}( \cfrac{ 1 }{ R_{0} } - \cfrac{ 1 }{ R_{L} } ) \)
切りくずを真っすぐに伸ばした時には,\( R_{L} \to \infty\)となり,次式が成立します.
\( \varepsilon_{B} \leq \cfrac{ t_{2} }{2}( \cfrac{ 1 }{ R_{0} } ) \)
最低でも,この条件が満たされない限りは,切りくずは分断されません.
よって,切りくず厚み\( t_{2} \)を大きくするか,切りくずの半径\( R_{0} \)を小さくすることで,条件を満たすことが必要です.
では,これがわかっていれば,切りくず分断が可能かというとそういうわけではないです.
切りくず厚み\( t_{2} \)が大きすぎると,切りくずの剛性が高すぎて変形しません.
切りくずの半径\( R_{0} \)が小さすぎると,切りくずのらせんが小さく,半径が広がるような変形が生じません.
あと,特に上記条件で難しいのは,そもそも\( R_{L} \)が,どのくらいまで変形させられるのか,ということです.
これは,切りくずが成長して,どこかに接触して\( R_{L} \)が大きくなったとしても,接触点が移動して接触状態が解消されて,切りくずに反力が与えられなくなる場合があるためです.
よって,\( R_{L} \)は\( R_{0} \)を基準として,ある程度の範囲でしか大きくなれないはずです.
その変化範囲で,切りくずを分断するには結構厳しい条件が必要になります.
ここでは,問題を片持ち梁で仮定して,上記関係性を簡単に検討します.
片持ち梁の先端に荷重が加えられて根元で破断が生じる場合の,先端での荷重と変位を計算します.
ここでは切りくずの断面は長方形であるとします.
\( F_{max} = \cfrac{ w h^{2} \sigma_{max} }{8L} \)
\( \delta_{max} = \cfrac{ 2 L^{2} \sigma_{max} }{3Eh} \)
\( h = \cfrac{ f_{r} }{ \tan( \theta_{s} )} \)
\( I = \cfrac{ w h^{3} }{ 12 } \)
\( \sigma_{max} \): 切りくずの引張強さ (800 MPa)
\( F_{max} \): 切りくず破断時の片持ち梁先端での荷重
\( \delta_{max} \): 切りくず破断時の片持ち梁先端での変位
\( h \): 切りくずの厚さ
\( w \): 切りくずの幅 (3 mm)
\( L \): 切りくずの長さ (1 mmから200 mm
\( E \): ヤング率 (210 GPa)
\( f_{r} \): 1回転当たりの送り量 (0.1, 0.2, 0.3, 0.4 mm/rev)
\( \theta_{s} \): せん断角 (25 degree)
\( I \): 断面二次モーメント
上記数値の仮定を各変数におき,実際に計算した結果を以下に示します. 1回転当たりの送り量\( f_{r} \)ごとに線を引いています.
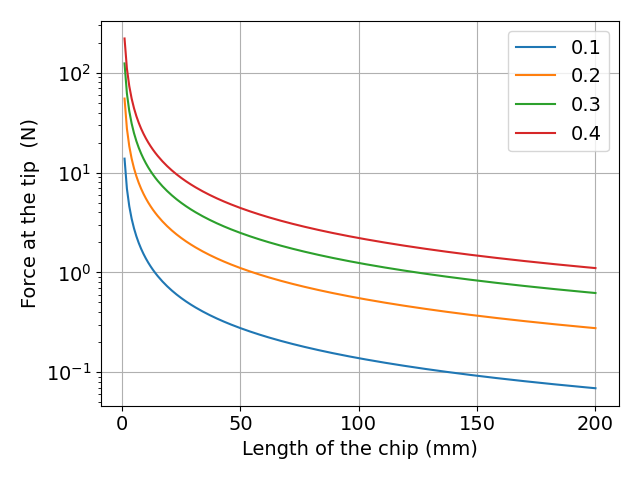
図 切りくず長さによる片持ち梁先端での荷重との関係
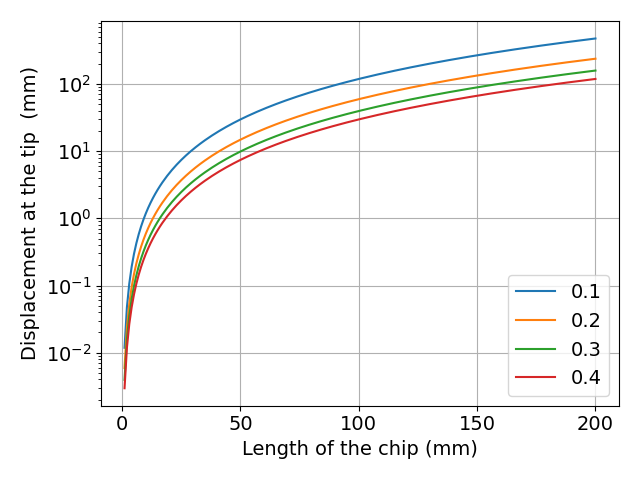
図 切りくず長さによる片持ち梁先端での変位との関係
数式からもわかりますが,切りくずが長くなると,破断に必要な荷重は小さくなり,変位は大きくなります.
今回の計算結果では,どちらかといえば,変位のほうが問題だと考えます.
切りくず長さが100mmになると,30mmから120mm程度の変位がなければ破断しません.
そんなに先端が動いたら,接触条件が変わるような気がします.
ついでに,切りくず長さに対して必要な変位の割合を計算してみます.
\( \cfrac{ \delta_{max} }{L} = \cfrac{ 2 L \sigma_{max} }{3Eh} \)
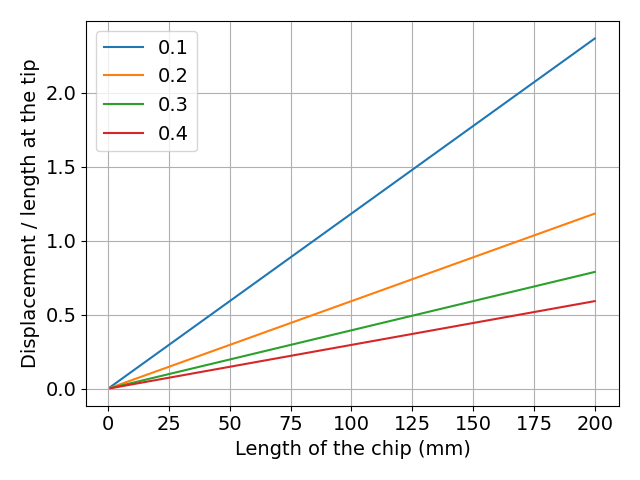
図 片持ち梁先端での変位/切りくず長さ
切りくずが長くなるほど,先端での変位も増えるので,破断が難しくなることがわかります.
よって,必要最小限の長さで切りくずの成長を拘束して,破断させることが重要だとわかります.