切削油剤の供給に関係する計算2
切削油剤を供給するときクーラントポンプの圧力を設定しますが,それでどのように供給量が決まるのでしょうか.
また,全長が長いドリルを付けたときに供給量が減っているように見えます.
そういった影響は,どのような関係式を使えば理解できるのでしょうか.
そのあたりを調べた結果について記載します.
基本はベルヌーイの式です.
\( \cfrac{v^2}{2g} + \cfrac{P}{\rho g} + h = H :const\)
\( v \): 流速
\( g \): 重力加速度
\( P \): 圧力
\( \rho \): 密度
\( h \): 高さ
\( H \): 全揚程
このベルヌーイの式が,1本の流線に沿って成り立ちます.
この性質を利用します.
切削油剤がタンクに溜まっていて,ポンプで送り出され,工作機械やツールホルダからなる管路を通過し,切削工具先端から吐出されます.
それを数式で表現すると次式のようになります.
\( \cfrac{P_{atom}}{\rho g} + H_{p} = \cfrac{v_{out}^2}{2g} + \cfrac{P_{atom}}{\rho g} + h_r \)
\( P_{atom} \): 大気圧
\( H_{p} \): クーラントポンプによって与えられるヘッド
\( v_{out} \): 吐出される切削油剤の流速
\( h_r \): 管路による損失ヘッド
上式で仮定しているのは,以下の条件です.
- クーラントタンクでは流速はゼロで,圧力は大気圧
- 切削工具先端で吐出されたときの圧力は大気圧
- 全ての構成要素の高さは同じ
理由は後で示されますが,\( H_{p} \)は放置しておいて,\( h_r \)を計算します.
管路内での損失ヘッドは,直管損失,曲がり損失,分岐損失など様々な要素で構成されます.
細かく考えると計算が複雑になるので,ここでは直管損失だけで計算します.
Y字型に分かれる管路を想定し,直管損失の要素として2つ考えます.
また,切削油剤としては水溶性のものを想定し,物性値には水の数値を使います.
- 共通管路=クーラントタンクから切削工具直前までの管路:直径30mm,長さ5m,本数1本
- 工具管路=切削工具から切削工具先端の吐出口までの管路:直径2mm,長さ50mm,100,250mmおよび500mm,本数2本(分岐)
\( h_r = \lambda \cfrac{L}{d} \cfrac{v^2}{2g} \)
\( = \lambda \cfrac{L}{d} \lbrace \cfrac{Q}{d^2 \pi / 4} \rbrace ^2 \cfrac{1}{2g} \)
\( = \lambda \cfrac{L}{d} \cfrac{16 Q^2}{d^4 \pi^2} \cfrac{1}{2g} \)
\( = \lambda \cfrac{L}{1} \cfrac{8 Q^2}{d^5 \pi^2} \cfrac{1}{g} \)
\( = \lambda \cfrac{L}{d^5} \cfrac{8 }{g \pi^2} Q^2 \)
\( \lambda \): 管摩擦係数
\( L \): 管の長さ
\( d \): 管の直径
\( Q \): 流量
\( \lambda = \lbrace 1.8 \log_{10}(\cfrac{R_e}{6.8}) \rbrace^{-2} \):ホワイトの式
管摩擦係数の式はレイノルズ数に応じていくつかありますが,ここではホワイトの式を用います.
\( 6 \cdot 10^3 \lt R_e \lt 4 \cdot 10^7 \)の範囲で用いられ,今回の場合は,この範囲に収まることは確認済みです.
切削工具から切削工具先端までの管路として,1本の管路から分岐した2本を仮定しています.
そのため,クーラントタンクから切削工具先端に到達して吐出される経路が2本あることになります.
この経路ごとにベルヌーイの式が成立することになります.
今回は,同じ形状の管路が2本あるだけなので,ポンプから供給された流量がちょうど半分ずつ流れることになります.
これを等量分岐といいます.
もし,異なる形状の管路を通る複数の経路がある場合,以下の条件を満たす流量を経路ごとに算出する必要があります.
- 全ての吐出口から出る流量の和は,ポンプからの供給量に等しい
\( Q_p = Q_{p1} + Q_{p2} + Q_{p3} + \ldots + Q_{pn} = \sum_{i=1}^{n} ( Q_{pi}) \)
- ポンプの全揚程は全ての経路で等しい
\( H_p = H_{p1} = H_{p2} = H_{p2}= \ldots = H_{pn} \)
これが配管流量の計算が難しい原因です.
等量分岐の場合は,その計算が不要なので,簡単に計算できます.
ということで,ここでは等量分岐を想定しているので,簡単に計算を行います.
ポンプからの供給量を\( Q_p \)としたとき,吐出口からは\( \cfrac{Q_p}{2} \)ずつ吐出されます.
これを用いて直管損失を計算します.
以下で使用している数値のうち,工作機械内部の配管を見たことはないので,共通管路の数値は根拠なしで決めてます.
- 共通管路=クーラントタンクから切削工具直前までの管路:直径30mm,長さ5m,本数1本
\( h_{r1} = \lambda \cfrac{L}{d^5} \cfrac{8 }{g \pi^2} Q_p^2 \)
\( = \lambda \cfrac{L}{d^5} \cfrac{8 }{g \pi^2} Q_p^2 \)
- 工具管路=切削工具から切削工具先端までの管路:直径2mm,長さ50mm,100,250mmおよび500mm,本数2本(分岐)
\( h_{r2} = \lambda \cfrac{L}{d^5} \cfrac{8 }{g \pi^2} ( \cfrac{Q_p}{2})^2 \)
\( H_{p} = \cfrac{v_{out}^2}{2g} + h_r \)
\( = \lbrace \cfrac{4 Q_p}{\pi d^2} \rbrace ^2 \cfrac{1}{2g} + h_{r1} + h_{r2} \)
\( = \cfrac{8}{\pi^2 d^4 g} Q_p^2 + h_{r1} + h_{r2} \)
ここまでやって得られたのは,ポンプの全揚程と流量の関係式です.
これだけでは結局,流量は決まりません.
次に,ポンプの性能曲線が必要になります.
ポンプの性能曲線は,下図に示すようなもので,ポンプの仕様として示されるものです.
下図の曲線は適当に決めたものなので,実在のポンプではありません.
比較のために,性能の違う性能曲線を2本引いています.
流量が増えると全揚程が下がる,という関係性にあることがわかります.
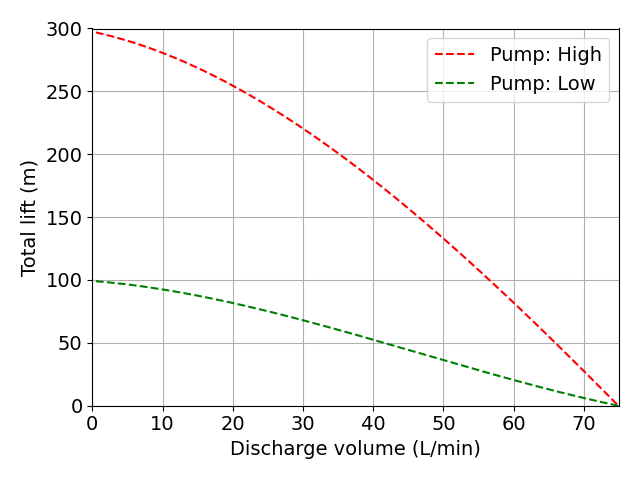
ポンプの性能をみるときは,輸送対象をどのくらいの高さまで運べるかというので揚程(高さ,単位:m)で評価するそうです.
また,輸送量ということで流量も\( L/min \)で評価するそうです.
なので,上図でもそのように表記しています.
この場合,ここまでの計算式内での流量の単位は\( m^3/s \)なのですが,グラフ表記をするときには\( L/min \)に変換しています.
あと,ついでに揚程と圧力の変換式についてもここに記載しておきます.
\( p = \rho g h \)
よって,水を対象としているときは,
\( p = 997 \cdot 9.8 \cdot h \)
\( = 9770.6 \cdot h \)
\( \risingdotseq 10^4 \cdot h \)
と書けるので,揚程1mは,圧力でいえば,約\( 10^4 \)Pa,つまり,約0.01MPaに相当します.
上図に,ポンプの全揚程と流量の関係式のグラフを追記します.
引いた曲線同士の交点が,ポンプの運転点になります.
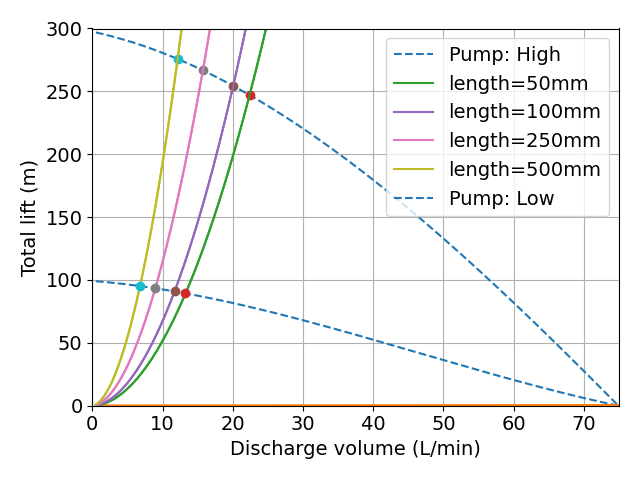
ポンプの性能曲線を2本,ドリルの長さを4種類想定しているので,交点が8個あります.
このグラフと計算結果からわかることをみていきます.
まず,管路ごとの抵抗の違いを比較します.
実際に流量を計算することで,各管路要素での損失が具体的に計算できます.
| ポンプ性能 | ドリル長さ (mm) |
ポンプ流量 (L/min) |
共通管路で 損失した揚程 (m) |
工具管路で 損失した揚程 (m) |
吐出口での流速として 保持している揚程 (m) |
|---|---|---|---|---|---|
| 低 | 50 | 13.25 | 0.03 | 25.73 | 62.98 |
| 低 | 100 | 11.70 | 0.02 | 41.39 | 49.11 |
| 低 | 250 | 8.95 | 0.01 | 64.74 | 28.74 |
| 低 | 500 | 95.14 | 0.01 | 80.06 | 16.59 |
| 高 | 50 | 22.40 | 0.07 | 64.49 | 180.00 |
| 高 | 100 | 20.05 | 0.06 | 106.23 | 144.22 |
| 高 | 250 | 15.75 | 0.04 | 174.08 | 89.00 |
| 高 | 500 | 12.15 | 0.02 | 221.08 | 52.96 |
まず,工具が長くなるにつれて,流量が減っていることがわかります.
これは,工具が長くなった分,損失が大きくなったためです.
次に,共通管路と工具管路を比較すると,工具管路での損失が明らかに大きいです.
共通管路のほうが,長さは10倍から100倍あり,直径は15倍あります.
直管損失の式を流量\( Q \)で整理した式を眺めると,長さは1乗ですが,直径が-5乗で効くことがわかります.
これにより,共通管路よりも,工具管路の直管損失が明らかに大きくなり,支配的な要因として作用しています.
次に,流速や,静圧と動圧の変化を比較します.
下表では圧力は揚程に単位を変換して表示しています.
| ポンプ性能 | ドリル長さ (mm) |
ポンプ流量 (L/min) |
吐出口 での流速 (m/s) |
ポンプ直後 での静圧 (m) |
ポンプ直後 での動圧 (m) |
吐出口 での動圧 (m) |
|---|---|---|---|---|---|---|
| 低 | 50 | 13.25 | 35.15 | 89.35 | 0.00 | 62.98 |
| 低 | 100 | 11.7 | 31.03 | 90.89 | 0.00 | 49.11 |
| 低 | 250 | 8.95 | 23.74 | 93.40 | 0.00 | 28.74 |
| 低 | 500 | 6.8 | 18.04 | 95.14 | 0.00 | 16.59 |
| 高 | 50 | 22.4 | 59.41 | 247.02 | 0.00 | 180.00 |
| 高 | 100 | 20.05 | 53.18 | 254.36 | 0.01 | 144.22 |
| 高 | 250 | 15.75 | 41.78 | 266.64 | 0.01 | 88.99 |
| 高 | 500 | 12.15 | 32.23 | 275.72 | 0.00 | 52.96 |
流量の低下に伴い,吐出口での流速も低下しています.
ポンプ直後では,管路直径が大きいため,静圧が高く,動圧が低いです.
実際には,ポンプ直後に圧力弁が設置されているはずなのですが,その動作をどう考慮したらいいのかわからないので,またわかったら追記します.
さきほど,直管損失に流量基準では直径が-5乗で効く,ということを書きました.
それでは,工具管路の直径を2mmではなく,4mmにするとどうなるのでしょうか.
計算した結果を下図に示します.
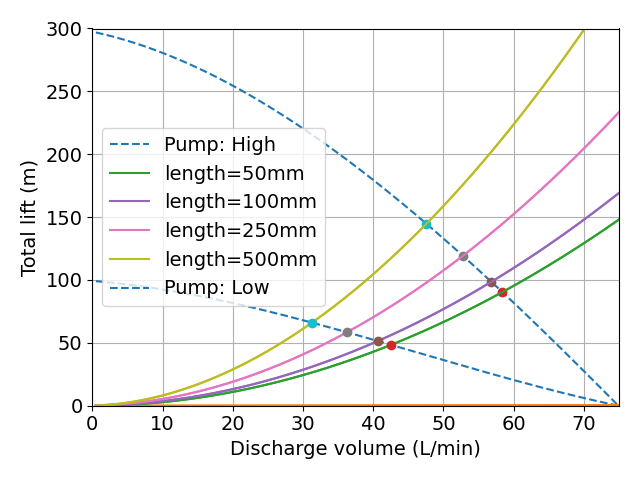
明らかに損失が低くなっていることがわかります.
工具管路の直径が2倍になっているので,ざっくり言えば,損失は32分の1に減少しているはずです.
| ポンプ性能 | ドリル長さ (mm) |
工具管路直径 (mm) |
ポンプ流量 (L/min) |
共通管路で 損失した揚程 (m) |
工具管路で 損失した揚程 (m) |
吐出口での流速として 保持している揚程 (m) |
|---|---|---|---|---|---|---|
| 低 | 50 | 2 | 13.25 | 0.03 | 25.73 | 62.98 |
| 低 | 50 | 4 | 42.50 | 0.21 | 7.35 | 40.50 |
| ポンプ性能 | ドリル長さ (mm) |
工具管路直径 (mm) |
ポンプ流量 (L/min) |
吐出口 での流速 (m/s) |
ポンプ直後 での静圧 (m) |
ポンプ直後 での動圧 (m) |
吐出口 での動圧 (m) |
|---|---|---|---|---|---|---|---|
| 低 | 50 | 2 | 13.25 | 35.15 | 89.35 | 0.00 | 62.98 |
| 低 | 50 | 4 | 42.50 | 28.18 | 48.38 | 0.05 | 40.50 |
しかしながら,約28%まで減少しています.
流量が増加した半面,吐出口の面積が増大したので,吐出口での流速は低くなっています.
流量は冷却能力に,流速は切りくずを流す能力に影響するので,トレードオフの関係になることがわかります.
これを解決するには,クーラントポンプの能力向上が楽だと思います.
次に,工具管路の本数を変更してみます.
工具管路の直径は2mm,長さは50mmで固定し,分岐後の本数を1本から4本に変化させます.
本数を変化させたときの計算結果を下図に示します.
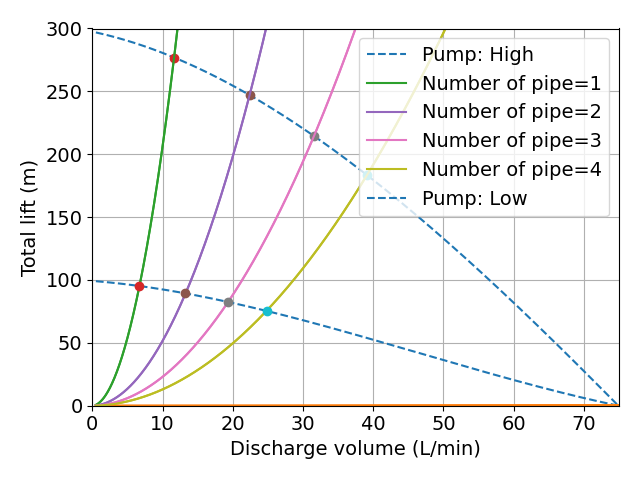
| ポンプ性能 | ドリル長さ (mm) |
分岐後本数 | ポンプ流量 (L/min) |
共通管路で 損失した揚程 (m) |
工具管路で 損失した揚程 (m) |
吐出口での流速として 保持している揚程 (m) |
|---|---|---|---|---|---|---|
| 低 | 50 | 1 | 6.70 | 0.01 | 31.20 | 64.42 |
| 低 | 50 | 2 | 13.25 | 0.03 | 25.73 | 62.98 |
| 低 | 50 | 3 | 19.35 | 0.05 | 22.18 | 59.70 |
| 低 | 50 | 4 | 24.80 | 0.08 | 19.26 | 55.16 |
| ポンプ性能 | ドリル長さ (mm) |
分岐後本数 | ポンプ流量 (L/min) |
吐出口 での流速 (m/s) |
ポンプ直後 での静圧 (m) |
ポンプ直後 での動圧 (m) |
吐出口 での動圧 (m) |
|---|---|---|---|---|---|---|---|
| 低 | 50 | 1 | 6.70 | 35.54 | 95.21 | 0.00 | 64.42 |
| 低 | 50 | 2 | 13.25 | 35.15 | 89.35 | 0.00 | 62.98 |
| 低 | 50 | 3 | 19.35 | 34.22 | 82.48 | 0.00 | 59.70 |
| 低 | 50 | 4 | 24.80 | 32.89 | 75.38 | 0.00 | 55.16 |
分岐後の管路本数を増やしたのに比例して,ポンプ流量も増加しているようにみえます.
しかしながら,吐出口での流速が徐々に低くなっているため,線形比例しているわけではないことがわかります.
戻る