切削速度ベクトルと送り速度ベクトルによる実1刃当たりの送り量の理解

フライス工具において，切削速度は工具の回転で生じ，送り速度は工具の移動で生じる，というのが通常の理解です．
送り速度は「工具」が工作物に食い込んでいく速度を定めています．
しかしながら，切削は刃先において行われることを考えると，刃先基準で切削速度と送り速度を考えるのが正しいはずです．
では，回転している刃先にとっての送り速度とは，どういう物理的な意味を持つのでしょうか．

まず，刃先基準で切削速度と送り速度を考えたとき，それを2次元切削のように描くと下図のようになります．



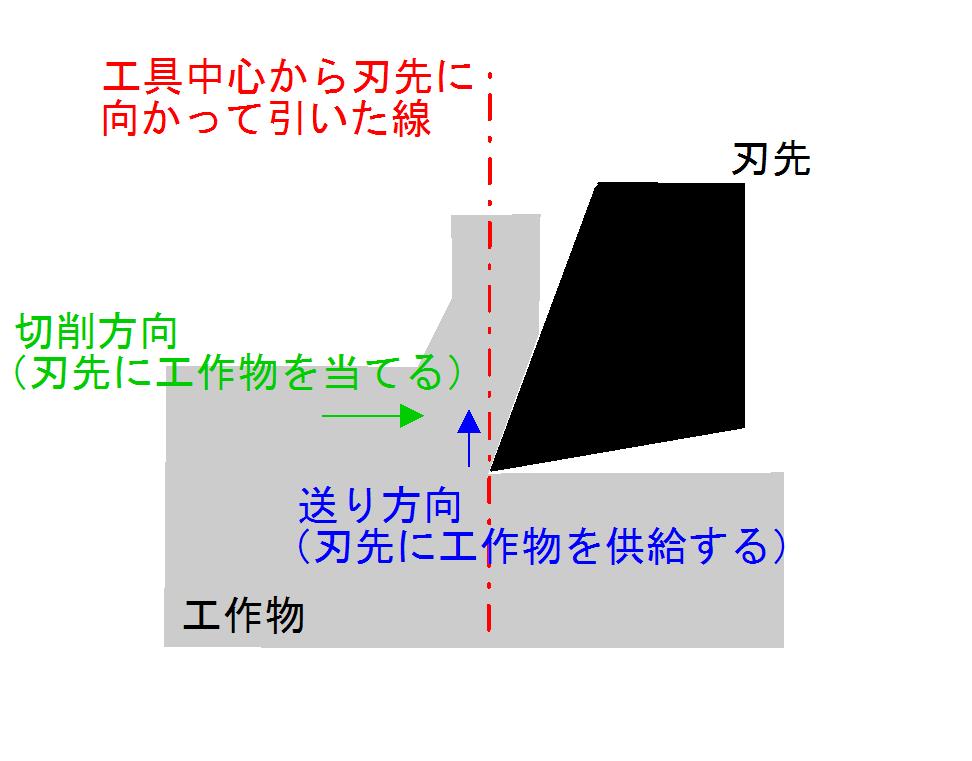
切削速度は，当然ながら，工作物が刃先に対して当たるときの速度を示します．
送り速度は，1刃当たりの送り量に主として影響します．
よって，1枚の刃先が工作物を除去したのち，次の刃が来るまでの間に，送り速度によって工作物が補充され，それが切り取り厚みになります．
フライス工具は回転しているので，上図を各刃先位置に並べると下図のようになります．



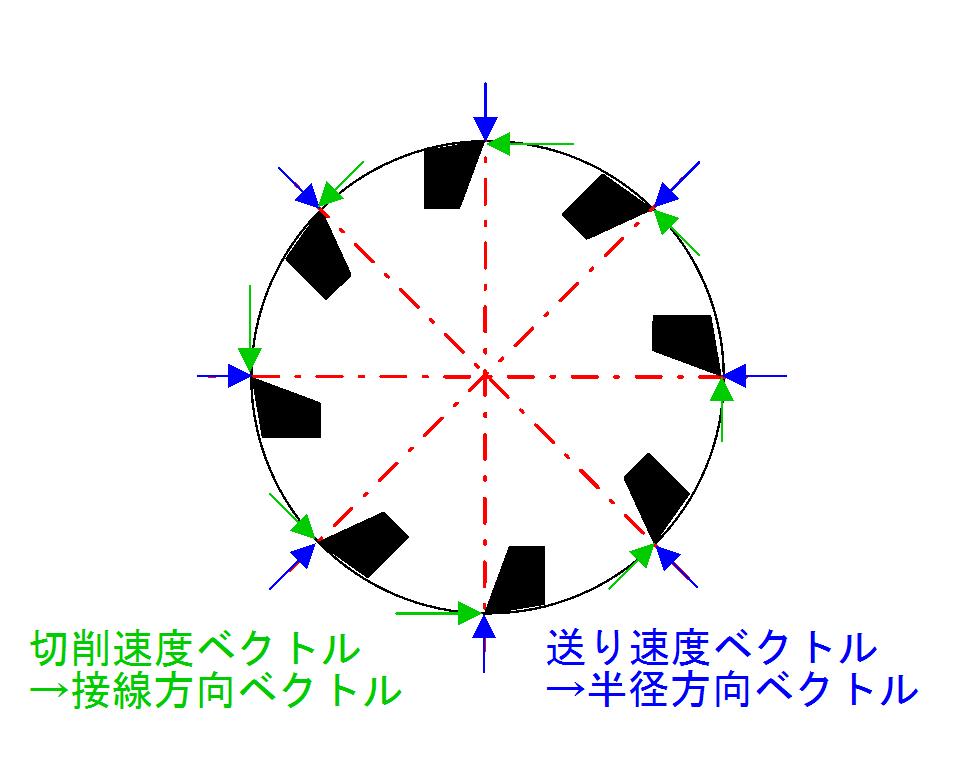
このような表記にすると，刃先基準での切削抵抗ベクトルと送り速度ベクトルが以下のように定義できることがわかります．
刃先基準での切削速度ベクトル：各刃先位置において工具直径が示す円の接線方向ベクトル．
刃先基準での送り速度ベクトル：各刃先位置において工具直径が示す円の中心に向かう半径方向ベクトル．

この定義を用いて，何ができるかといわれると難しいのですが，試しに実1刃当たりの送り量と，実切削速度の計算を行ってみます．
まず，下図のように，右回りに回転しているフライス工具に対して，Y軸負方向に向かって速度を持つ工作物が接近してくる状態を想定します．



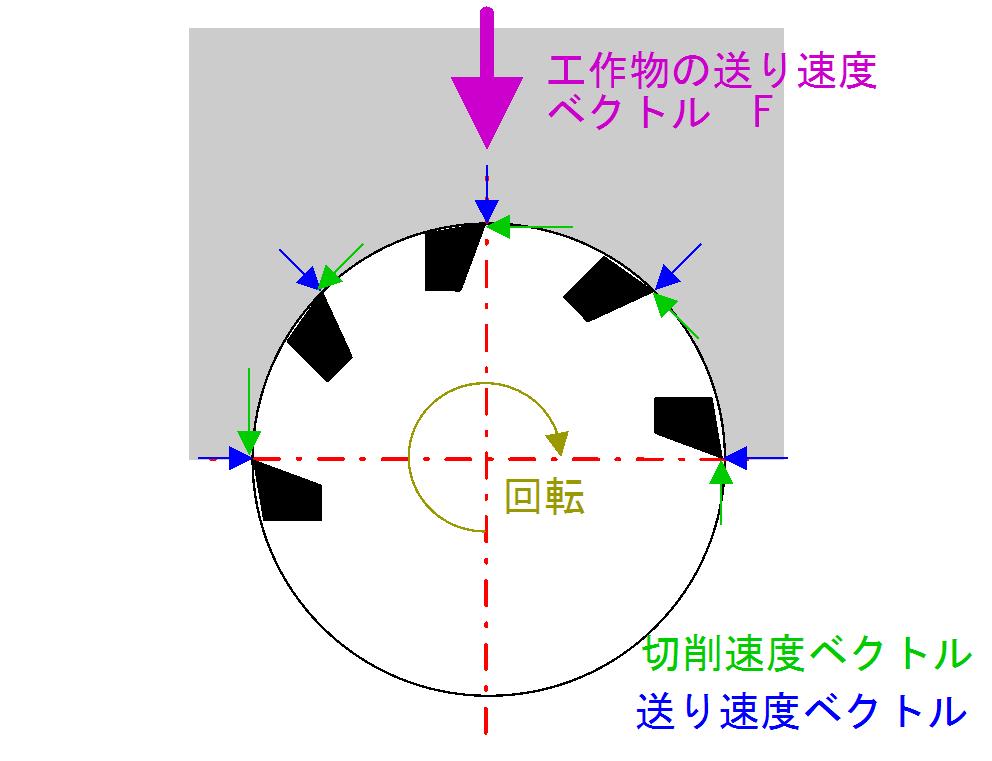
まず，刃先位置点Pの座標を次式によって示します．
\( P_{e} = (r\cos(-\omega t + \pi),r\sin(-\omega t + \pi)) \)
\( \omega = \cfrac{2 \pi S}{60} \)

\( P_{e} \): 切れ刃先端の座標
\( r \): 工具半径
\( \omega \): 工具の角速度
\( t \): 時間　ただし，\( 0 \leq t \leq \cfrac{\pi}{\omega} \)

この座標を微分すると，工具回転によって点Pがもつ接線速度ベクトル\( \vec{V_p} \)が得られます．
\( \vec{V}_{p} = (r\omega\sin(-\omega t + \pi),-r\omega\cos(-\omega t + \pi)) \)

工作物が軸負方向に向かって速度を持つので，その速度ベクトルを次式で示します．
\( \vec{F}_{w} = (0,-F) \)

\( F \): 工作物の送り速度

工具回転による点Pでの接線速度ベクトル\( \vec{V_c} \)と，工作物の送り速度ベクトル\( \vec{F_w} \)から，各刃先位置において工作物が刃先に向かう合成速度ベクトルを計算します．
\( \vec{v}_{all} = -\vec{V}_{p} + \vec{F}_{w} = (-r\omega\sin(-\omega t + \pi),+r\omega\cos(-\omega t + \pi)-F) \)
この合成速度ベクトルから，刃先位置点Pにおいて，すくい面に向かう方向の接線方向成分と，工具中心に向かう成分を取り出します．
そのために，内積を使うので，2種類の単位ベクトルを用意します．
\( \vec{e}_{tangent} = (-\sin(-\omega t + \pi),\cos(-\omega t + \pi)) \)
\( \vec{e}_{center} = (-\cos(-\omega t + \pi),-\sin(-\omega t + \pi)) \)

\( \vec{e}_{tangent} \): 刃先位置点Pにおいて，すくい面に向かう方向の接線方向単位ベクトル
\( \vec{e}_{center} \): 刃先位置点Pにおいて工具中心に向かう単位ベクトル

\( \vec{v}_{all} \)と\( \vec{e}_{tangent} \)との内積を計算すると，刃先基準での切削速度，つまり，実切削速度が得られます．
\( \vec{v}_{all} \cdot \vec{e}_{tangent} = r \omega - F \cos( - \omega t + \pi ) \)
\( r \omega \)は，工具半径と回転数から計算される，通常の切削速度です．
それに対して，刃先位置によって送り速度が足されたり引かれたりする形になっています．
溝加工でいうところの，刃先が食いつくところでは和，刃先が離脱するところでは差の形で作用するので，計算しなくてもわかる程度の内容です．
そのうえ，実用上は，切削速度と送り速度間に差がありすぎて，\( r \omega \)のみでほとんど決まるため，計算する意味がないです．
計算する意味があるのは，極端な小径エンドミルや，ボールエンドミルの中心付近だけです．

次に，\( \vec{v}_{all} \)と\( \vec{e}_{cirvle} \)との内積を計算すると，刃先基準での送り速度，つまり，実送り速度が得られます．
\( \vec{v}_{all} \cdot \vec{e}_{circle} = F \sin( - \omega t + \pi ) \)
これは刃先に実際に作用している送り速度であって，実1刃当たりの送り量\( f_{zreal} \)とは異なりますので，回転数Sと刃数Zを使って計算を進めます．
\( f_{zreal} = \cfrac{ F \sin( - \omega t + \pi )}{SZ} \)
通常使われる1刃当たりの送り量\( f_{z} \)の定義は，次式のとおりです．
\( f_{z} = \cfrac{ F }{SZ} \)
よって，次式のように書き直せます．
\( f_{zreal} = f_{z} \sin( - \omega t + \pi ) \)
これにより，実1刃当たりの送り量が1刃当たりの送り量にsin関数をかけると求められる，というこちらもよくある結果が導出できました．

結局，元から知ってる計算式が導出できただけなのですが，それが導出できたということは刃先基準での切削速度ベクトルと送り速度ベクトルの考え方が間違ってないということを示唆すると思います．
通常のフライス加工だとこんなことを考える必要はないのですが，ミルターニングなど，工具と工作物が同時に動くような場合には，何が切削速度で何が送り速度なのかを考える必要があるので，そういうときにベクトルによる理解が使えるはずです．