変位,速度および加速度の測定に関して
切削工具や工作物の振動を測定することがあります.
振動を測定するには,変位,速度および加速度の3種の物理量のどれかとして測定することになります.
この振動を単振動として数式で表現した場合,次式で表されます.
\(\displaystyle d = A \sin ( \omega t) \)
\(\displaystyle v = A \omega \cos ( \omega t) \)
\(\displaystyle a = -A \omega^2\sin ( \omega t) \)
\(\displaystyle \omega = 2 \pi f \)
\( d \): 変位
\( v \): 速度
\( a \): 加速度
\( A \): 片振幅
\( \omega \): 周波数(radian)
\( t \): 時間
\( f \): 周波数(Hz)
上式より,各物理量での最大値には片振幅と周波数が影響することがわかります.
また,周波数の影響の仕方が,変位,速度および加速度で異なることがわかります.
そこで,周波数に対する物理量の大きさの変化を1つのグラフにおさめると下図のようになります.
図 周波数に対する変位,速度および加速度の変化
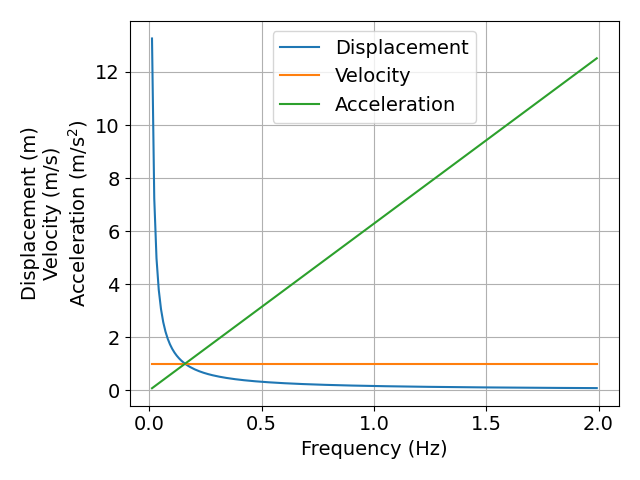
上図では,振動のエネルギを一定として考えることとしています.
この場合,次式より,速度一定が必要となることがわかります.
\(\displaystyle E = \cfrac{1}{2} m v^2 \)
\( E \): エネルギ
\( m \): 質量
この仮定によって,上図では,速度が一定となっています.
また,このように図示すると,低周波数領域では変位が,高周波数領域では加速度が相対的に大きくなることがわかります.
つまり,変位,速度および加速度では,得意とする周波数領域が異なる,ということがわかります.
ここまでの話の流れは,書籍や他のウェブサイトにも記載がよくあります.
ここで問題なのは,各物理量を測定するためのセンサの性能との併記がなされていないことです.
つまり,高周波領域で加速度が有利だったとしても,加速度センサにその高周波領域を測定できるだけの性能がなければ意味がないのでは?ということです.
そこで,いくつかのセンサの性能をざっくり調査した結果をグラフ内に描きこんだものを作成しました.
切削加工においては,加工誤差への影響が重要であるため,下図では変位を一定としています.
図中に記載されている3本の直線は,青色が1mm,橙色が1μm,緑色が1nmの変位を示しています.
調査したセンサの種類は以下のとおりです.
- 変位センサ:レーザ変位センサ,渦電流式変位センサ,静電容量型変位センサ
- 速度センサ:レーザドップラー振動計
- 加速度センサ:MEMS用加速度センサ,単軸加速度センサ
各センサの対応可能な範囲を1つの領域として塗りつぶしています.
塗りつぶされた領域の,縦軸の最大値が測定範囲の最大値,縦軸の最小値が分解能,横軸の最大最小は測定可能な周波数範囲を示しています.
周波数範囲は,本来は周波数応答曲線に従って記入したかったのですが,そこまでの記載がないものが多かったので,記載のあるサンプリング周波数から決めたものもあります.
当然ながら,この世に存在するすべてのセンサを調べたわけではないので,あくまで参考程度の図として捉えてください.
図 周波数と変位の関係
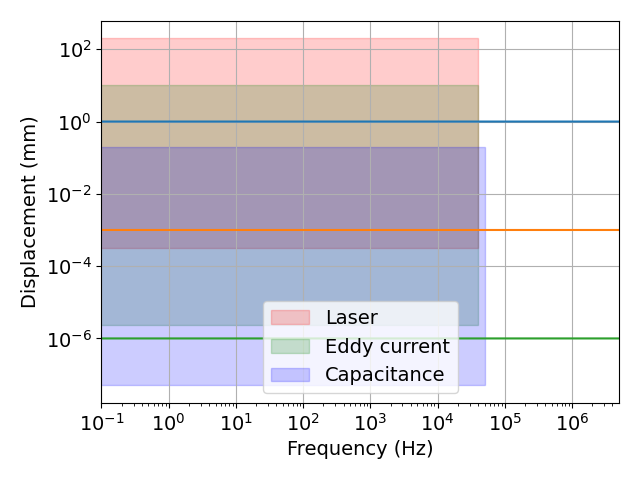
図 周波数と速度の関係
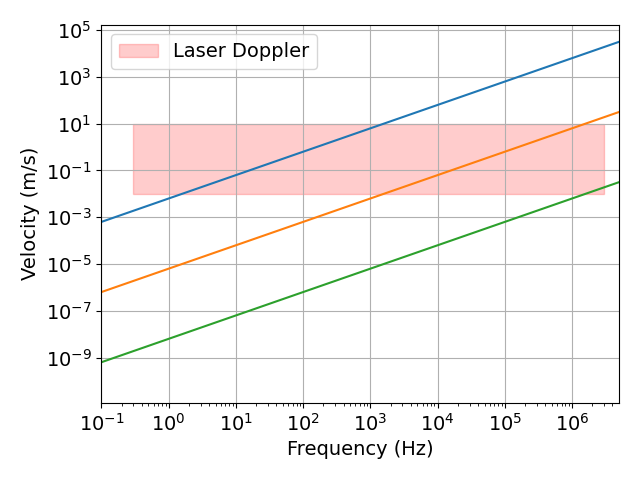
図 周波数と加速度の関係
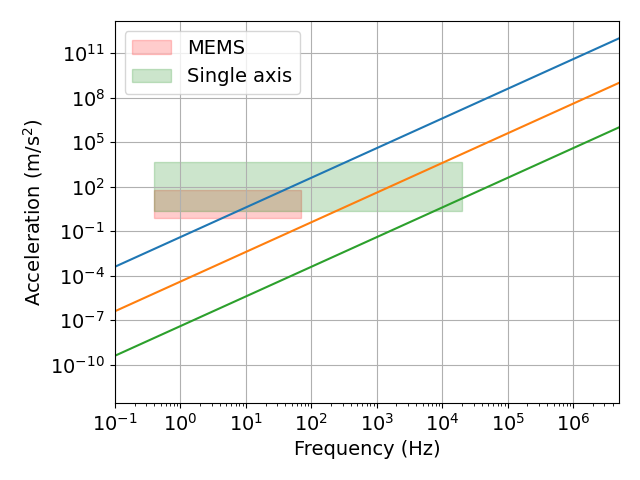
これらの図より,以下のことがわかります.
- nmオーダの変位は,変位センサでないと測定するのが難しい.
- 速度と加速度では低周波数領域の振動が測定できない.
戻る