角度基準と半径方向切込み深さ基準における切削抵抗と仕事率

フライス加工における切削動力の計算式は次式で示されます．

\( P = \cfrac{ap \cdot ae \cdot V_{f} \cdot K_{c}}{60 \cdot 10^6 \cdot \eta} \)

この計算式を見ていて不思議に思っていたことが2つあります．
1つ目は，半径方向切込み深さに対して線形に切削動力が増加するのかどうか．
2つ目は，切り取り厚みを考慮したときにも同じような形になるのかどうか．
これを調べるために，計算してみたいと思います．

まず，比切削抵抗を定数1つであらわすモデルを使った場合の計算式を作ります．
想定する加工状況は，肩削りのアップカットとします．

\( F_{1} = K_{1} \cdot ap \cdot fz \cdot \sin( \theta ) \)

\( F_{1} \): 切削抵抗
\( K_{1} \): 比切削抵抗
\( ap \): 軸方向切込み深さ
\( fz \): 1刃当たりの送り量
\( \theta \): 回転角

ある1枚の刃先による任意の瞬間の切削抵抗である\( F_{1} \)を工具回転に沿って積分すれば仕事になります．
\( W_{1} = \int F_{1} R d \theta = K_{1} \cdot R \cdot ap \cdot fz \cdot ( \cos( \theta_{e}) - \cos(\theta_{d}) ) \)

\( W_{1} \): 切削加工による仕事
\( R \): 工具半径
\( \theta_{e} \): 食いつき角 (rad)
\( \theta_{d} \): 離脱角 (rad)

アップカットを想定しているので，食いつき角\( \theta_{e} = 0 \)とします．
その結果，次式が得られます．
\( W_{1} = K_{1} \cdot R \cdot ap \cdot fz \cdot ( 1 - \cos(\theta_{d}) ) \)
これに回転数と刃数をかけると仕事率，つまり，切削動力になります．
\( P_{1} = Z \cdot \cfrac{S}{60} \cdot K_{1} \cdot R \cdot ap \cdot fz \cdot ( 1 - \cos(\theta_{d}) ) \)

\( P_{1} \): 切削動力
\( Z \): 刃数
\( S \): 回転数 (rpm)

次に，比切削抵抗を2つの定数で示すモデルで計算してみます．

\( F_{2} = K_{2a} \cdot ap \cdot fz \cdot \sin( \theta ) + K_{2b} \cdot ap \)

\( K_{2a} \): 切削面積で決まる切削抵抗成分の比切削抵抗
\( K_{2b} \): 切れ刃稜線の長さで決まる切削抵抗成分の比切削抵抗

\( W_{2} = \int F_{2} R d \theta = K_{2a} \cdot R \cdot ap \cdot fz \cdot ( \cos( \theta_{e}) - \cos(\theta_{d}) ) + K_{2b} \cdot ap \cdot R (\theta_{d} - \theta_{e} ) \)
ここでもアップカットを想定しているので，食いつき角\( \theta_{e} = 0 \)とします．
\( W_{2} = K_{2a} \cdot R \cdot ap \cdot fz \cdot ( 1 - \cos(\theta_{d}) ) + K_{2b} \cdot ap \cdot R \cdot \theta_{d} \)
これに回転数と刃数をかけると仕事率，つまり，切削動力になります．
\( P_{2} = Z \cdot \cfrac{S}{60} \cdot ( K_{2a} \cdot R \cdot ap \cdot fz \cdot ( 1 - \cos(\theta_{d}) ) + K_{2b} \cdot ap \cdot R \cdot \theta_{d} ) \)

これで2つの比切削抵抗モデルでの切削抵抗と仕事，仕事率が計算できるようになりました．
具体的な数値を代入して，切削抵抗と仕事率をグラフにしてみます．

\( K_{1} = 1840 \): 比切削抵抗 (MPa)
\( K_{2a} = 1518 \): 比切削抵抗 (MPa)
\( K_{2b} = 48 \): 比切削抵抗 (MPa)
\( ap = 1 \): 軸方向切込み深さ (mm)
\( fz = 0.3 \): 1刃当たりの送り量 (mm/t)
\( R = 50 \): 工具半径 (mm)
\( Z = 4 \): 刃数
\( S = 600 \): 回転数 (rpm)

まず，横軸を離脱角にとったときの計算結果を示します．


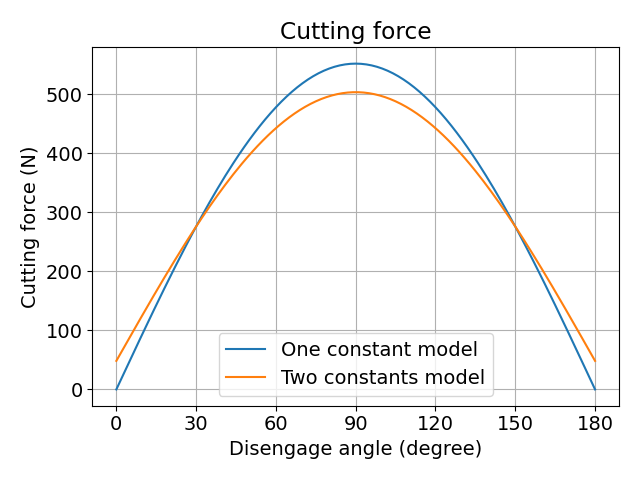
図　離脱角による切削抵抗の変化


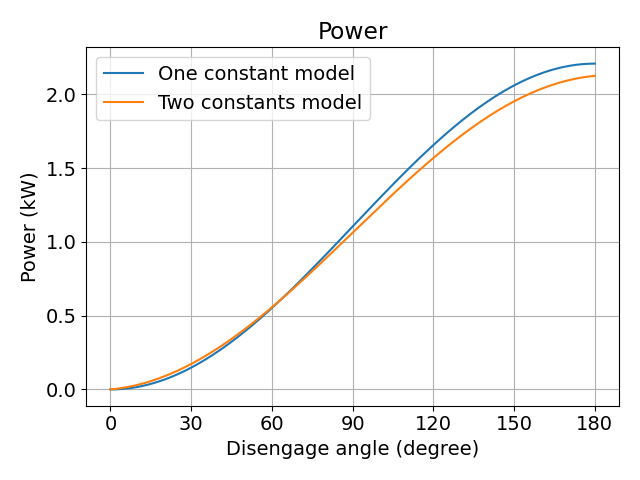
図　離脱角による切削動力（仕事率）の変化

切削抵抗の計算結果のほうはサインカーブを描いており，まぁ，想像どおりといった感じです．
切削動力ではどちらのモデルでも計算結果はほぼ同じような変化をしていて，三角関数の影響を受けていそうな，非線形な変化をしています．

次に，肝心の，半径方向切込み深さに対しての変化の様子を確認します．
そのために，次式を用いて離脱角を半径方向切込み深さに変換し，それを横軸に使います．
\( ae = R ( 1 - \cos(\theta_{d})) \)

少し脱線しますが，上式を使って\( P_{1} \)と\( P_{2} \)の式変形をすると次式が得られます．
\( P_{1} = Z \cdot \cfrac{S}{60} \cdot K_{1} \cdot ap \cdot fz \cdot ae \)
\( P_{2} = Z \cdot \cfrac{S}{60} \cdot ( K_{2a} \cdot ap \cdot fz \cdot ae + K_{2b} \cdot ap \cdot R \cdot \theta_{d} ) \)
ここで，
\( V_{f} = Z \cdot fz \cdot S \)
の関係式を用いると，
\( P_{1} = \cfrac{V_{f}}{60} \cdot K_{1} \cdot ap \cdot ae \)
となり，これは，このページの最初に示した数式と機械効率\( \eta \)以外の項が同じになります．
つまり，この切削動力の数式は，比切削抵抗については定数1個で表現しており，実切り取り厚みによる影響は考慮していないということがわかります．


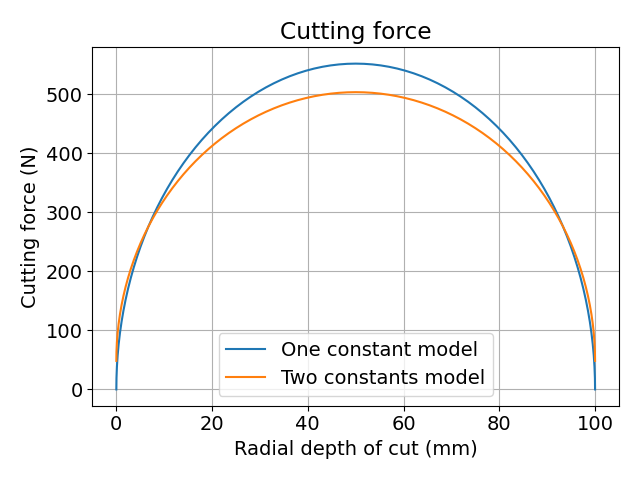
図　半径方向切込み深さによる切削抵抗の変化


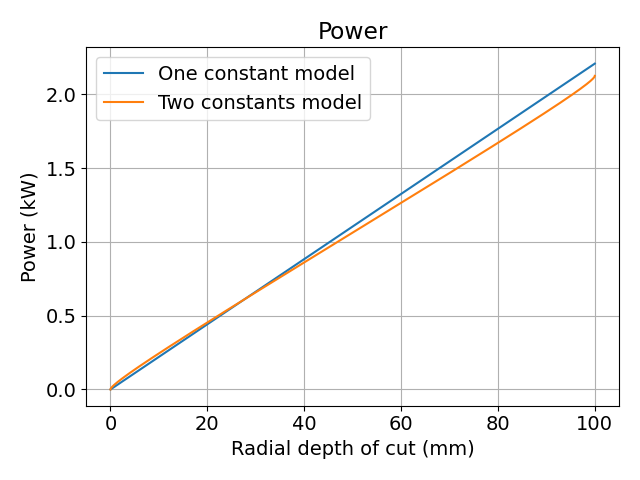
図　半径方向切込み深さによる切削動力（仕事率）の変化

こちらで見てみると，仕事率は半径方向切込み深さに対して線形変化していると言っても問題なさそうなくらいに見えます．
特に，比切削抵抗を1つの定数で示しているほうは線形です．
さきほど式変形した結果でも，aeを変数としてみたとき，\( P_{1} \)は線形の数式になっていました．
よって，半径方向切込み深さに対して線形で切削動力は増えると覚えておいても大きく外れないと思います．
2つのモデルで使っている数値は，fzが0から0.3の値をとるときに平均値が同じ値になるように決定しているので，計算結果のオーダが略同等になるのはそれが理由です．
ただし，2種のモデルはところどころ形状は違っているので，まぁそんなもんかなと思いました．