丸コーナ上での切削抵抗ベクトルの変化傾向
旋削工具の丸コーナのコーナ半径はR0.2からR3.2くらいまであります.
コーナ半径が大きいと背分力が大きくなるとかいう話をよく聞きます.
実際,加工してみるとそんな感じなのですが,具体的にはどのくらい変わるのでしょうか.
ここでは,厳密な計算ではないですが,なんとなくの定量的な評価をしてみます.
丸コーナでの加工では,切り取り厚さが位置によって変化することを考慮する必要があります.
まずは手始めに切削面積\( A \)を計算します.
下図に示すような丸コーナによる旋削を想定します.
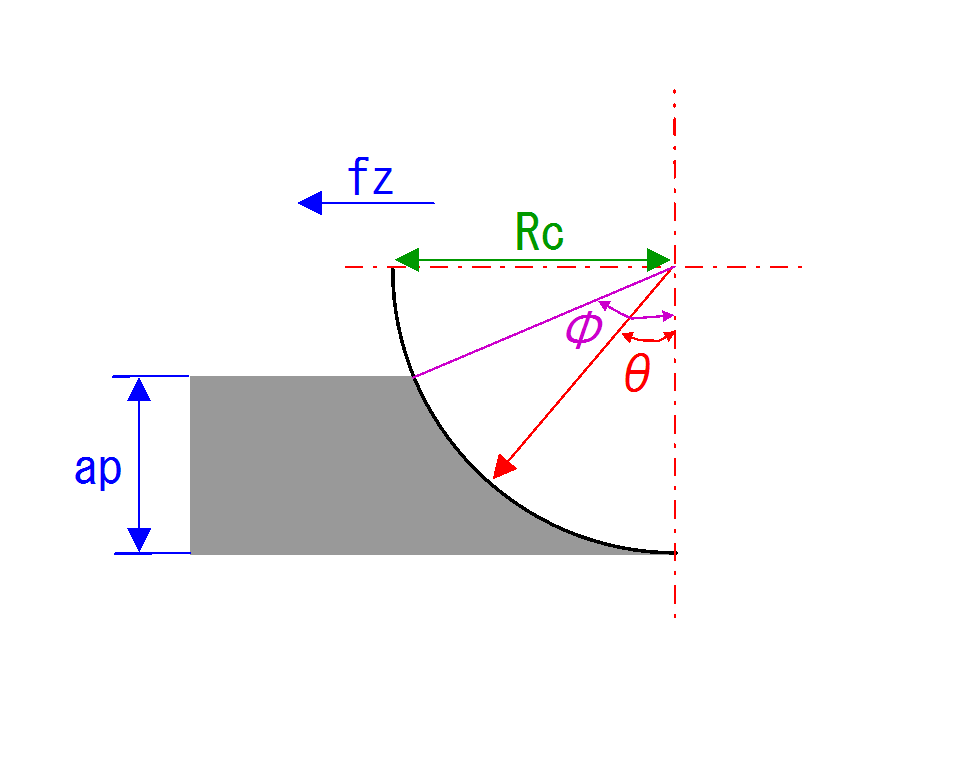
図 丸コーナでの旋削
\( A = \int_0^\phi f_{z} \sin{(\theta)} R_{c} d \theta \)
\( f_{z} \): 1回転当たりの送り量
\( R_{c} \): コーナ半径
\( \phi \): 切込み量の端点を示す角度
\( a_{p} \): 切込み量
ここでは,\( a_{p} = R_{c} (1 - \cos{(\phi)}) \)の関係性が満たされます.
上式を以下のように解きます.
\( A = f_{z} R_{c} \int_0^\phi \sin{(\theta)} d \theta \)
\( A = f_{z} R_{c} (1 - \cos{(\phi)}) \)
ここで,\( a_{p} = R_{c} (1 - \cos{(\phi)}) \)より,
\( A = f_{z} a_{p} \)
切り取り厚さの分布から計算しても切削面積は\( f_{z} \)と\( a_{p} \)から定まるという当たり前の結果が出ました.
これは,正方形をずらして平行四辺形にしても面積が変わらないのと同じ理屈なので,特に面白くもありません.
では,上式を用いて,切れ刃の各微小部位において,切れ刃に垂直な方向に切削抵抗ベクトルが生じるものとして,切れ刃全体に生じる切削抵抗ベクトルを計算します.
各微小部位での切削抵抗ベクトルをX方向(送り分力方向)とY方向(背分力方向)に分けて計算することで切削抵抗ベクトルを得ます.
比切削抵抗には,切削面積の比切削抵抗\( K_{a} \)と切れ刃長さの比切削抵抗\( K_{e} \)の2つを用いるモデルを使います.
送り分力\( F_{x} \)を次式で導出します.
\( F_{x} = \int_0^\phi K_{a} f_{z} \sin{(\theta)} R_{c} \sin{(\theta)} d \theta + \int_0^\phi K_{e} R_{c} \sin{(\theta)} d \theta \)
\( F_{x} = K_{a} f_{z} R_{c} \int_0^\phi \sin^2{(\theta)} d \theta + K_{e} R_{c} \int_0^\phi \sin{(\theta)} d \theta \)
\( F_{x} = K_{a} f_{z} R_{c} \int_0^\phi \cfrac{ 1- \cos{(2\theta)}}{2} d \theta + K_{e} R_{c} \int_0^\phi \sin{(\theta)} d \theta \)
\( F_{x} = \cfrac{K_{a} f_{z} R_{c}}{4} \{ 2\phi - \sin{(2\phi)} \} + K_{e}R_{c} \{ 1 - \cos{(\phi)} \} \)
背分力\( F_{y} \)を次式で導出します.
\( F_{y} = \int_0^\phi K_{a} f_{z} \sin{(\theta)} R_{c} \cos{(\theta)} d \theta + \int_0^\phi K_{e} R_{c} \cos{(\theta)} d \theta \)
\( F_{y} = K_{a} f_{z} R_{c} \int_0^\phi \sin{(\theta)} \cos{(\theta)} d \theta + K_{e} R_{c} \int_0^\phi \cos{(\theta)} d \theta \)
\( F_{y} = K_{a} f_{z} R_{c} \int_0^\phi \cfrac{ \sin{(2\theta)} }{2} d \theta + K_{e} R_{c} \int_0^\phi \cos{(\theta)} d \theta \)
\( F_{y} = \cfrac{ K_{a} f_{z} R_{c} }{4} \{ 1 - \cos{(2\phi)} \} + K_{e} R_{c} \sin{(\phi)} \)
次に,上式に数値を代入して,その変化を確認します.
適当にS45Cの切削を想定したような比切削抵抗を用います.
- 比切削抵抗1つのモデル:\( K_{a} = 2000 \),\( K_{e} = 0 \)
- 比切削抵抗2つのモデル:\( K_{a} = 1580 \),\( K_{e} = 48.4 \)
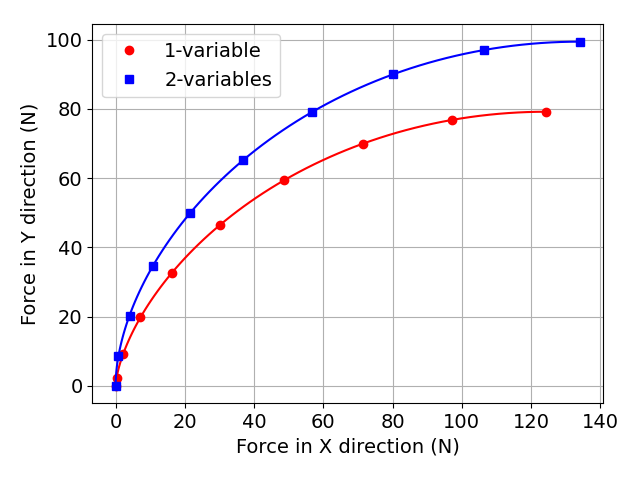
図 送り分力\( F_{x} \)と背分力\( F_{y} \)の変化
*マーカは\( \phi \)が0度から90度まで10度刻みのときの計算結果を示します.
*よって,上図中の原点上にあるマーカが\( \phi = \)0度,原点から最も離れたマーカが\( \phi = \)90度を示します.
*Fxは送り分力であり,上図「図 丸コーナでの旋削」における+X方向,つまり,fzで示している送り方向とは逆の方向を示します.
*Fyは背分力であり,上図「図 丸コーナでの旋削」における紙面上方向,つまり,+Y方向を示します.
切削抵抗ベクトルから方向の情報だけを抜き出した図を以下に示します.
角度は\( \arctan(\cfrac{ F_{y} }{ F_{x} }) \)によって算出しています.
参考までにColwell則による切りくず流出方向の角度を併記しています.
Colwell則による方向の角度は\( \cfrac{ \pi }{2} - \cfrac{ \phi }{2} \)で算出できます.
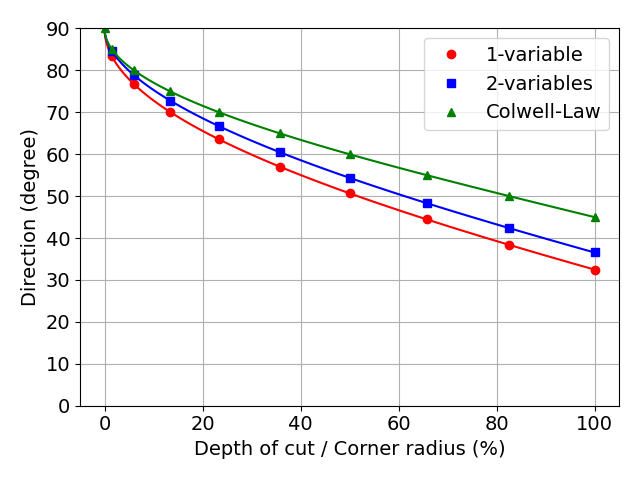
図 切込み量による切削抵抗ベクトルの方向の変化
*縦軸での90度は背分力方向で上図「図 丸コーナでの旋削」における紙面上方向,つまり,+Y方向を示します.
*縦軸での0度は送り分力方向で上図「図 丸コーナでの旋削」における+X方向,つまり,fzで示している送り方向とは逆の方向を示します.
上図より,今回の仮定で算出される切削抵抗ベクトルは,Colwell則の方向よりも送り分力方向を向くことがわかります.
それでは,次に比切削抵抗2つのモデルを用いて,同じ切込み量に対してコーナ半径を変更した場合を計算します.
コーナ半径は0.2mmから3.2mmで8種類,1回転あたりの送り量は0.1mm/t,切込み量は0mmから0.2mmとします.
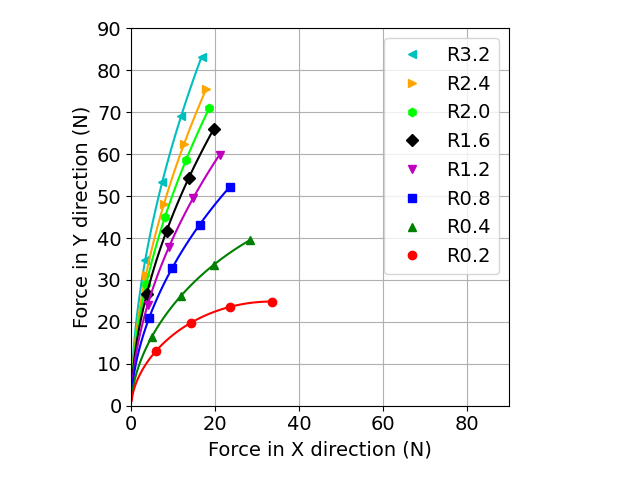
図 コーナ半径による切削抵抗ベクトルの変化
*マーカは切込み量が0.05mm,0.10mm,0.15mm,0.20mmでの計算結果を示します.
切込み量0.2mmにおいて,コーナ半径0.2mmと3.2mmでは切削抵抗ベクトルの方向が明らかに違うことがわかります.
また,コーナ半径が大きいと,切り取り厚さが薄くなるため,比切削抵抗が高い領域を使うことになり,切削抵抗ベクトルの大きさも大きくなっています.
工作物が変形しやすい背分力方向に切削抵抗ベクトルが向いて,かつ,大きさも大きくなってしまうので,工作物変位が増大するように見えます.
実際の切削現象はここまで単純ではありませんが,単純なモデルでもここまで変化が出るのは知っていても損はないと思います.