質量と剛性,減衰による周波数応答への影響
ある系を加振したときに発生する振動が大きいという問題があったと仮定します.
このとき,周波数応答の応答倍率を下げることによって振動を抑えたいとしたとき,質量と剛性,減衰のどれが有効なのでしょうか.
「よくわかる機械の制振設計」に同じようなことは書いてあるのですが,固有振動数と励振周波数の関係性についての記述が少なく,個人的に腑に落ちない点がありました.
そこで,1自由度振動系の応答倍率を計算し,その結果から自分なりに考えてみることにしました.
1自由度振動系の計算には,ミリングマニアックで使用したものと同じものを使います.
\(\displaystyle \omega_0 = \sqrt{ \cfrac{k}{m} } \)
\(\displaystyle c_c = 2\sqrt{ mk } \)
\(\displaystyle \zeta = \cfrac{c}{c_c} \)
\( \omega_0 \):固有角振動数
\( c_c \):臨界減衰
\( \zeta \):減衰比
\( m \):質量
\( c \):減衰
\( k \):剛性
解析対象を力励振の周波数応答とします.
このとき,共振角振動数と応答倍率,位相は次式によって示されます.
\(\displaystyle \omega_r = \omega_0 \sqrt{ 1-2\zeta^2} \)
\(\displaystyle A = \cfrac{1}{ \sqrt{ (1- (\cfrac{\omega}{\omega_0})^2 )^2 + 4\zeta^2(\cfrac{\omega}{\omega_0})^2 ) } } \)
\(\displaystyle \phi = \arctan( \cfrac{ 2\zeta\cfrac{\omega}{\omega_0} }{1-(\cfrac{\omega}{\omega_0})^2} ) \)
\( \omega_r \):共振角振動数
\( A \):応答倍率
\( \phi \):位相
\( \omega \):励振周波数
上式にある応答倍率と位相の式を使って検証をします.
そのためには,質量と剛性,減衰に何らかの数値が必要です.
「工作機械の振動特性の解析と最適設計」の262ページに横型フライス盤の共振振動数,モーダルフレキシビリティ,等価減衰比があるので,ここから逆算して試算に使用します.
逆算結果を以下に示します.
\( m = 6.2 \cdot 10^{4} \):質量(kg)
\( k = 1.33 \cdot 10^{10} \):剛性 (N/m)
\( c = 5.55 \cdot 10^{5} \):減衰 (kg/s)
ここまでが計算の下準備です.
次に,質量と剛性,減衰の各項目を独立して80%,100%,120%にした条件で,応答倍率と位相を計算します.
応答倍率に関しては,100%にしたときの計算結果を基準とし,80%と120%にしたときの,応答倍率比も計算します.
計算結果のグラフを以下に示します.
- 質量変化
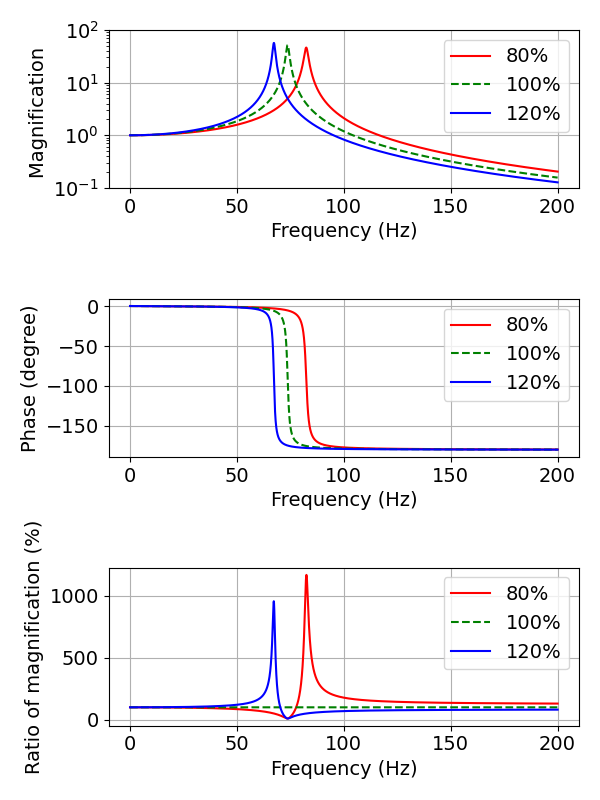
- 剛性変化
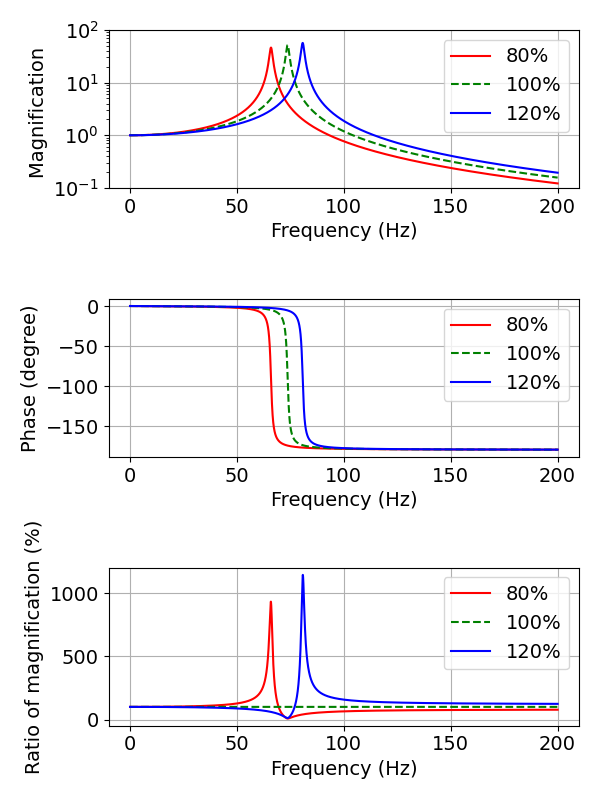
- 減衰変化
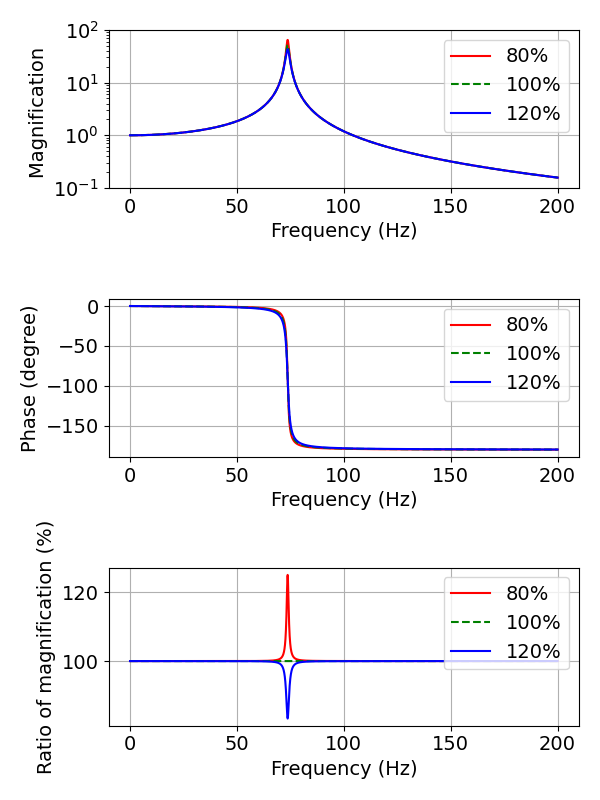
3つのグラフを見比べたときに,わかりやすいところから言及すると,減衰を増やすと,固有振動数の位置は同じで,その応答倍率だけが小さくなります.
よって,減衰を大きくしておけば,共振が生じたときにも,その応答倍率を抑えられることがわかります.
質量と剛性を変えた結果を見比べると,両者はほぼ同じであるように見えます.
しかしながら,よく見ると,変数を80%にしたときの変化と,変数を120%にしたときの変化が入れ替わっていることがわかります.
この結果は,固有振動数に対して,励振周波数が高いか低いかによって,質量と剛性の増減の方針を変える必要があることを示唆しています.
固有振動数よりも励振周波数が低い場合は,質量を小さくするか,剛性を高くすることで,応答倍率を下げることができます.
固有振動数よりも励振周波数が高い場合は,質量を大きくするか,剛性を低くすることで,応答倍率を下げることができます.
よって,まず最初に重要なのは,問題としている振動モードを特定し,その固有振動数と励振周波数を比較し,その大小関係を特定することです.
次に,上記方針に従って,応答倍率を低減することで,振動を抑えることができます.
上記のやり方は,共振が発生していないことが条件です.
共振が生じている場合は,固有振動数と励振周波数を一致させないように励振周波数や剛性,質量を変える.
もしくは,減衰を足して応答倍率を下げる方針になります.
参考資料:
- 三好孝典:よくわかる機械の制振設計,日刊工業新聞社,2018,pp.53-56.
- 芳村敏夫,横山隆,日野順市:基礎振動工学,共立出版株式会社,1992.
- 吉村允孝:工作機械の振動特性の解析と最適設計,学位論文(京都大学),1976,p.262.
戻る