切削抵抗と摩擦角,せん断抵抗,せん断角
下図に示す2次元切削での切削抵抗ベクトルを使って,切削抵抗が摩擦角やせん断抵抗,せん断角とどういった関係にあるかを導出する過程があります.
このページでは,その流れをなぞってみたいと思います.
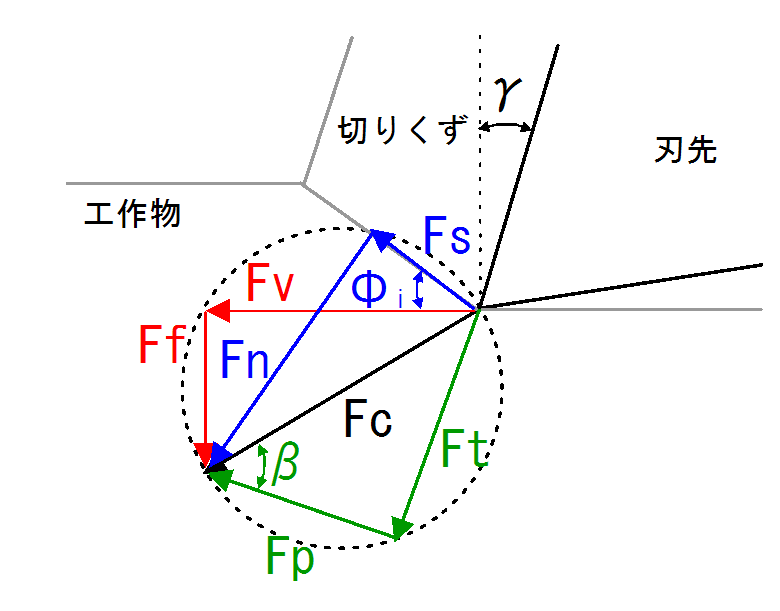
\( F_{c} \): 切削抵抗(主分力と背分力の合力)
\( F_{v} \): 切削抵抗(主分力)
\( F_{f} \): 切削抵抗(背分力)
\( F_{p} \): 切削抵抗のすくい面に対する垂直
\( F_{t} \): 切削抵抗のすくい面に対する水平成分(すくい面上での摩擦力)
\( F_{s} \): せん断面での平均せん断抵抗
\( F_{n} \): せん断面にかかる平均垂直応力
\( \beta \): 摩擦角
\( \mu \): 摩擦係数
\( \gamma \): すくい角
\( \phi_{i} \): せん断角
上図に書いてある円は\( F_{c} \)を直径とする円です.
これにより\( F_{v} \)と\( F_{f} \),\( F_{p} \)と\( F_{t} \),\( F_{s} \)と\( F_{n} \)はそれぞれ直交関係にあることがわかります.
*図中の切削抵抗の向きが,どうみても切削力なのは無視してください.
3つの荷重の組は下記の意味を持つと考えます.
まず,切削抵抗と摩擦角の関係性を導出します.
そのために\( F_{v} \)-\( F_{f} \)表記と\( F_{p} \)-\( F_{t} \)表記の関係性を示します.
\( F_{v} \)-\( F_{f} \)を座標系と捉えたとき,\( F_{p} \)-\( F_{t} \)は\( -\gamma \)回転した位置にあります.
よって,これは座標系の回転として関連付けられるので,次式が成立します.
\( \begin{bmatrix} F_{p} \\ F_{t} \end{bmatrix} = \begin{bmatrix} \cos(\gamma) & -\sin(\gamma) \\ \sin(\gamma) & \cos(\gamma) \end{bmatrix}\begin{bmatrix} F_{v} \\ F_{f} \end{bmatrix}\)
\( F_{p} = F_{v}\cos(\gamma) - F_{f}\sin(\gamma) \)
\( F_{t} = F_{v}\sin(\gamma) + F_{f}\cos(\gamma) \)
これにより摩擦係数\( \mu \)と摩擦角\( \beta \)は次式で求められます.
\( \mu = \tan(\beta)= \cfrac{F_{t}}{F_{p}} = \cfrac{F_{v}\sin(\gamma) + F_{f}\cos(\gamma)}{F_{v}\cos(\gamma) - F_{f}\sin(\gamma)} \)
この式の意味するところは,切削抵抗を測定して,すくい角がわかれば,摩擦係数\( \mu \)と摩擦角\( \beta \)が決定できるということです.
これらは被削材とすくい面の材質との親和性を解析するのに使えるのかもしれません.
次に,せん断抵抗と切削抵抗の関連性を導出します.
そのために\( F_{v} \)-\( F_{f} \)表記と\( F_{s} \)-\( F_{n} \)表記の関係性を示します.
これも座標回転で解釈できて,\( F_{v} \)-\( F_{f} \)を座標系と捉えたとき,\( F_{s} \)-\( F_{n} \)は\( -\phi_{i} \)回転した位置にあります.
よって,次式が成立します.
\( \begin{bmatrix} F_{s} \\ F_{n} \end{bmatrix} = \begin{bmatrix} \cos(\phi_{i}) & -\sin(\phi_{i}) \\ \sin(\phi_{i}) & \cos(\phi_{i}) \end{bmatrix}\begin{bmatrix} F_{v} \\ F_{f} \end{bmatrix}\)
\( F_{s} = F_{v}\cos(\phi_{i}) - F_{f}\sin(\phi_{i}) \)
\( F_{n} = F_{v}\sin(\phi_{i}) + F_{f}\cos(\phi_{i}) \)
ここで,せん断面の面積を\( A_{s} \)とし,切削面積を\( A \)とすると次式が成立します.
\( A = A_{s}\sin(\phi_{i}) \)
よって,
\( A_{s} = \cfrac{A}{\sin(\phi_{i})} \)
となります.
このせん断面の面積\( A_{s} \)を使うと,せん断面での抵抗を応力に変換できます.
\( \tau_{s} = \cfrac{F_{s}}{A_{s}} = \cfrac{F_{s}\sin(\phi_{i})}{A} = \cfrac{ \lbrace F_{v}\cos(\phi_{i}) - F_{f}\sin(\phi_{i})\rbrace \sin(\phi_{i}) }{A} \)
\( \sigma_{s} = \cfrac{F_{n}}{A_{s}} = \cfrac{ \lbrace F_{v}\sin(\phi_{i}) + F_{f}\cos(\phi_{i}) \rbrace \sin(\phi_{i}) }{A} \)
この式が何に使えるかというと,2つの使い方があります.
1つ目は切削抵抗を測定し,切りくずの厚み\( h_{c} \)の測定結果と,切込み深さ\( h \),すくい角\( \gamma \)を次式に代入してせん断角\( \phi_{i} \)を求めれば,せん断面でのせん断応力と垂直応力を計算できます.
\( \tan(\phi_{i}) = \cfrac{ h\cos(\gamma) }{ h_{c} - h\sin(\gamma) } \)
もう1つはせん断抵抗\( \tau_{s} \)を物性値と捉えることで,ここから切削抵抗が逆算できます.
そこで,せん断抵抗\( \tau_{s} \),摩擦角\( \beta \),せん断角\( \phi_{i} \),すくい角\( \gamma \)の4つを既知とした場合の切削抵抗\( F_{v} \)-\( F_{f} \)を導出します.
切削抵抗ベクトル\( F_{c} \)と\( F_{s} \)のなす角度は幾何的に\( \phi_{i} + \beta - \gamma \)となるので,次式が成立します.
\( F_{n} = \tan(\phi_{i} + \beta - \gamma)F_{s} \)
今度は\( F_{s} \)-\( F_{n} \)から\( F_{v} \)-\( F_{f} \)への変換として,座標変換の要領で式を立てると,次式が得られます.
\( \begin{bmatrix} F_{v} \\ F_{f} \end{bmatrix} = \begin{bmatrix} \cos(-\phi_{i}) & -\sin(-\phi_{i}) \\ \sin(-\phi_{i}) & \cos(-\phi_{i}) \end{bmatrix}\begin{bmatrix} F_{s} \\ F_{n} \end{bmatrix}\)
より,
\( F_{v} = F_{s}\cos(\phi_{i}) + F_{n}\sin(\phi_{i}) \)
\( F_{f} = -F_{s}\sin(\phi_{i}) + F_{n}\cos(\phi_{i}) \)
まず,\( F_{v} \)を導出します.
そのために次式を用います.
\( \tau_{s} = \cfrac{F_{s}\sin(\phi_{i})}{A} \)
これを書き換えると次式になります.
\( F_{s} = \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
よって,次式も成立します.
\( F_{n} = \tan(\phi_{i} + \beta - \gamma)\cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
これらを代入すると,
\( F_{v} = \cfrac{A\tau_{s}}{\sin(\phi_{i})}\cos(\phi_{i}) + \tan(\phi_{i} + \beta - \gamma)\cfrac{\tau_{s}A}{\sin(\phi_{i})}\sin(\phi_{i}) \)
\( F_{v} = \lbrace \cos(\phi_{i}) + \tan(\phi_{i} + \beta - \gamma)\sin(\phi_{i}) \rbrace \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
\( F_{v} = \cfrac{ \cos(\phi_{i} + \beta - \gamma)\cos(\phi_{i}) + \sin(\phi_{i} + \beta - \gamma)\sin(\phi_{i}) }{\cos(\phi_{i} + \beta - \gamma)} \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
ここで,
\( \cos(X-Y) = \cos(X)\cos(Y) + \sin(X)\sin(Y) \)
の関係を使い,
\( F_{v} = \cfrac{ \cos\lbrace \phi_{i} - (\phi_{i} + \beta - \gamma) \rbrace}{\cos(\phi_{i} + \beta - \gamma)} \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
\( F_{v} = \cfrac{ \cos( - \beta + \gamma) }{\cos(\phi_{i} + \beta - \gamma)} \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
ここで
\( \cos(X) = \cos(-X) \)
の関係を使うと,
\( F_{v} = \cfrac{ \cos( \beta - \gamma) }{\cos(\phi_{i} + \beta - \gamma)} \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
となります.
次に\( F_{f} \)を求めます.
\( F_{f} = \tan(\beta - \gamma)F_{v} \)
\( F_{f} = \cfrac{ \sin( \beta - \gamma) }{\cos(\phi_{i} + \beta - \gamma)} \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
切削抵抗\( F_{c} \)は\( F_{v} \)と\( F_{f} \)の合力なので,
\( F_{c} = \cfrac{ 1 }{\cos(\phi_{i} + \beta - \gamma)} \cfrac{\tau_{s}A}{\sin(\phi_{i})} \)
として導出できます.
これで,もしも,せん断抵抗\( \tau_{s} \),摩擦角\( \beta \),せん断角\( \phi_{i} \),すくい角\( \gamma \)がわかれば,切削抵抗がわかるという理論式が得られました.
せん断抵抗は被削材の物性値,摩擦角は被削材と工具の相性などで決まる数値,すくい角は工具形状で決まる,となれば,せん断角を求められるようにすればいいだけにみえます.
そうして,せん断角の関係式を作る流れになり,Merchantの第1の方程式やLee-Shafferの式が作られたのだと考えます.
ただし,実際のところは,これらの既知とした数値もよくわからないので,切削抵抗もわからない,といった感じです.
次に,「この既知とした数値もよくわからない」というのが具体的にどういったものであるかを,以下に示します.
まず,せん断抵抗です.
せん断抵抗は「せん断線図の最大荷重をせん断切り口面の総面積で割った値」を意味し,引張強さの80%の値で近似されるそうです.
これなら物性値として一定値で扱えそうな気がしますが,そうではありません.
このせん断抵抗は,ひずみ速度依存性と温度依存性を持ち,それらによって変化してしまうことが大きな問題です.
切削加工でのひずみ速度が102 s-1や104 s-1であるのに対し,引張試験機のひずみ速度は10-3 s-1や10-1 s-1程度と桁が異なります.
また,切削加工では加工点の温度も数百度に達するため,室温とは全く異なる環境です.
よって,通常の引張試験機で取得された数値を,上記切削理論式に適用しても利用しても意味がないです.
そのため,SHPB(Split Hopkinson Pressure Bar)試験などで,高ひずみと高温度を再現して取得されたデータを活用するのが正しいです.
SHPB試験の結果から,Johnson-Cookモデルなどのひずみ速度と温度を考慮した応力-ひずみ関係式の係数を同定して切削シミュレーションに組み込む,という手法が市販のソフトウェアでは取られています.
実切削で得られた切削抵抗からせん断抵抗を取得しても良いですが,そうなると切削試験なしに切削抵抗は得られないことになります.
次に摩擦角です.
摩擦角は「接触する二面間に働く摩擦力とそのときの接触面に垂直に作用する荷重の合力が,垂直荷重とのなす角」を意味します.
通常の摩擦角であれば,二面を構成する物質の親和性や表面性状によって一定値として得られます.
しかしながら,切削加工においては,高圧力と高温度が問題になります.
切削加工では比切削抵抗の値を参照すれば,500MPaから4000MPa程度の高い圧力がすくい面上にかかっています.
このような環境下では,摩擦力の上限がせん断抵抗になるとかいった説(要確認)もあり,摩擦角も一定値として扱うのは難しいです.
唯一わかるのは,すくい角と言いたいところですが,それも難しい場合があります.
切れ刃先端部には超硬工具では数十μmの丸みがあるため,切込み量が同程度の場合は,すくい角の設定が困難になります.
よって,刃先の丸みに対して十分な大きさの切込み量であるか,単結晶ダイヤモンドのような丸みが極端に小さい工具材質である必要があります.
よって,実用的には使えないということになるのですが,切削理論の基本部分にはなっているので,知っていれば何かの役に立つこともあるかと思います.
参考文献:
- 精密工学講座 切削工学,コロナ社,p292
- 塑性加工技術シリーズ12 せん断加工-プラス加工の基本技術-,コロナ社,p.18
- 臼井英治, 白樫高洋, 益子正己,高速圧縮試験と二, 三の結果 切削における温度・ひずみ速度効果の基礎的研究 (第1報)
- G.R.Johnson and W.H.Cook: Fracture characteristics of three metals subjected to various strain, strain rate, temperatures and pressures, Engineering Fracture Mechanics, Vol.21, No.1, pp.31-48, 1985
- 立矢宏, 駒形雄一, 放生明廣, 茶谷明義,温度およびひずみ速度依存性を考慮した炭素鋼の動的構成式の決定