空転によるドリルの破壊
L/Dが大きいドリル,つまり,長いドリルを使うとき,空転させるとドリルが遠心力で曲がって折れることがあります.
そのため,長いドリルは下穴をあけておいて,そこにドリル先端を低速回転状態で入れてから,切削速度まで回転数を上げるのが普通です.
ここで疑問に思うのは,L/Dがどのくらいのときに,下穴が必要になるのでしょうか.
それについて,多少いい加減ではありますが,計算してみます.
問題を設定して解くために,以下の3つの仮定というか設定を行います.
-
回転物をドリルではなく円柱として考えます.
これは単純に,ドリルの断面形状を私が把握していないからです.
-
円柱の中心軸と,回転軸に対して偏心しているものとします.
これは,円柱の中心軸と回転軸が完全に一致している場合は,遠心力による曲げが生じないからです.
また,現実において,円柱の中心軸と回転軸が完全に一致しているなんて事象はあり得ないので,妥当な仮定でもあります.
-
偏心した円柱を回転させて遠心力が生じている状況を想像します.
片持ち梁を曲げるがごとく,円柱が曲がるわけですが,このとき遠心力は回転軸からの距離の二乗に比例します.
これを数式に落とし込んでみるとわかるのですが,計算式が簡単に解けるような形ではなく,私では円柱の変位が求められません.
数式が解ける人は,ここから先は読む必要はないと思います.
このページでは,円柱全体に生じる遠心力は,円柱の自由端先端に加わるものとして計算を行います.
この場合,円柱の破壊の観点からすると,安全側の計算になります.
問題としては,円柱全体の質量が円柱の自由端に集中質量として存在しており,円柱に生じる遠心力と変位が釣り合っているような状況を想定することになります.
片持ち梁先端の変位の大きさは次式で得られます.
\( \Delta r = \cfrac{F_{r}L^3}{2EI}\)
\( \Delta r\):片持ち梁自由端での変位量
\( F_{r} \):遠心力
\( L \):片持ち梁の長さ
\( E \):ヤング率
\( I \):断面二次モーメント
遠心力は次式で得られます.
\( F_{r} = (\epsilon + \Delta r)m\omega^2\)
\( \epsilon \):片持ち梁の中心軸が回転軸に対して偏心している量
\( m \):片持ち梁の質量
\( \omega \):角速度
この2つの式を組み合わせると次式が得られます.
\( F_{r} = \cfrac{\epsilon}{ \cfrac{1}{m\omega^2} - \cfrac{L^3}{2EI} } \)
この片持ち梁先端変位と遠心力が釣り合った条件下において,円柱根元での最大曲げ応力が引張り強さを越えなければ破壊は生じません.
ですので,ここから円柱根元での最大曲げ応力を計算します.
\( \sigma_{max} = \cfrac{M}{Z} = \cfrac{ F_{r}L }{ Z }\)
ここに\( F_{r} \)の数式を代入すると,
\( \sigma_{max} = \cfrac{L}{Z} \cfrac{\epsilon}{ \cfrac{1}{m\omega^2} - \cfrac{L^3}{2EI} } \)
となる.
ここで,\( \sigma_{max} \)を引張強さ\( \sigma_{B} \)で置き換えて,回転数を求めれば,遠心力による破壊が生じる回転数が求められます.
\( \omega = \sqrt{ \cfrac{1}{ mL ( \cfrac{ \epsilon }{Z \sigma_{B}} + \cfrac{L^2}{2EI} ) } } \)
\( \omega \)の単位はrad/sなので,次式を用いればrpmに変換することができます.
\( S = \cfrac{60\omega}{2\pi} = \cfrac{60}{2\pi} \sqrt{ \cfrac{1}{ mL ( \cfrac{ \epsilon }{Z \sigma_{B}} + \cfrac{L^2}{2EI} ) } } \)
円柱の直径を5mm,10mmm,15mmの3種とし,円柱の長さによって,遠心力による破壊が生じる回転数がどのように変化するかをグラフ化します.
材質を超硬合金とし,密度を15g/cm3,引張強さ\( \sigma_{B} \)を1000MPaとします.
偏心量\( \epsilon \)は1μmとします.
断面二次モーメントや断面係数は円柱として計算されうるものを用いるので,次式のとおりになります.
\( A = \cfrac{\pi D^2 }{4} \)
\( I = \cfrac{\pi D^4}{64} \)
\( Z = \cfrac{I}{D/2} = \cfrac{\pi D^3}{32} \)
\( m = \rho L A = \cfrac{\rho L \pi D^2 }{4} \)
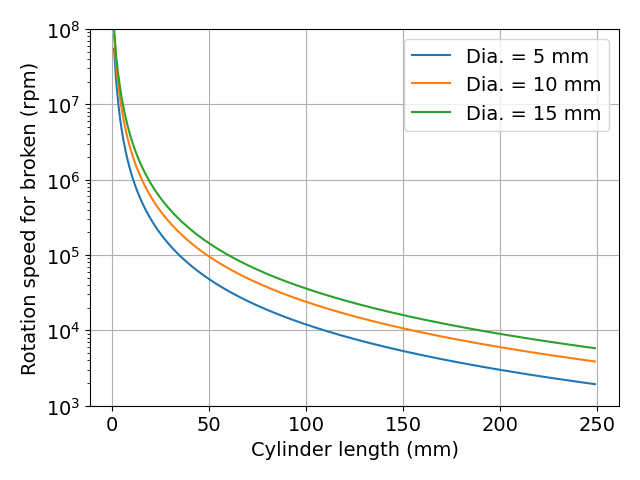
図 円柱の長さと,遠心力による破壊が生じる回転数の関係
円柱直径を工具径と捉えると,工具径が変わっている場合,回転数が同じでも切削速度が異なります.
また,工具径や長さが変わるときは,よくL/Dが指標として使われます.
ですので,切削速度を縦軸として用いたり,L/Dを横軸として用いて,同じグラフを描き替えてみます.
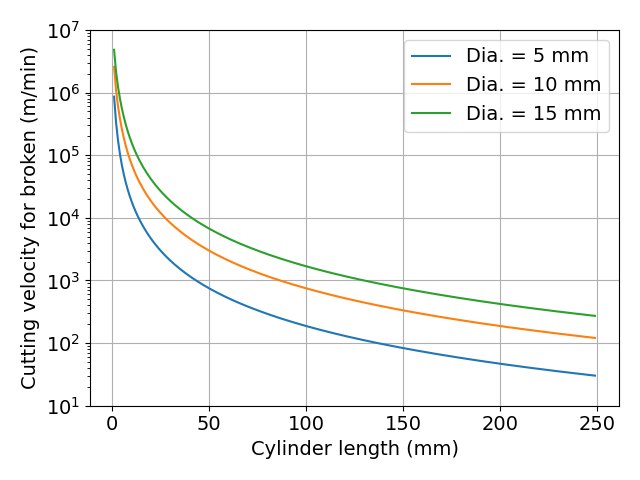
図 円柱の長さと,切削速度の関係
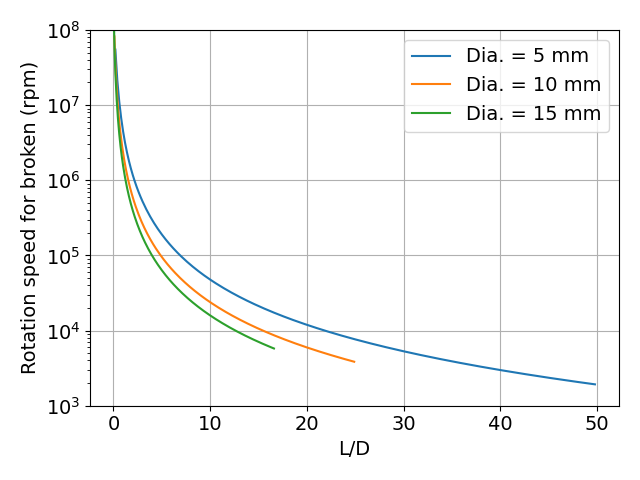
図 L/Dと,遠心力による破壊が生じる回転数の関係
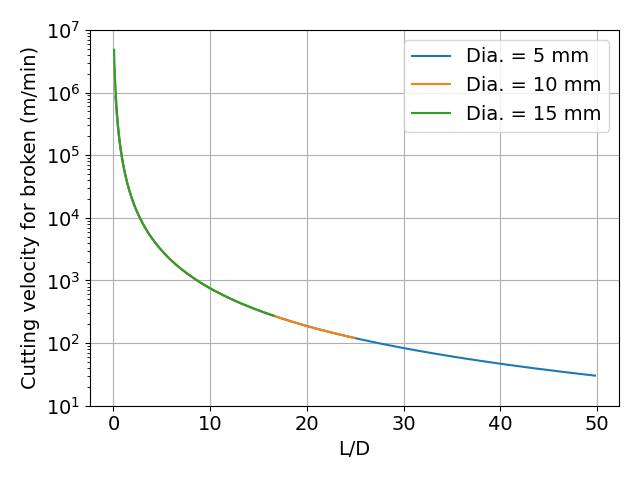
図 L/Dと,切削速度の関係
L/Dと切削速度の関係で整理したときだけ,工具径3種の線が同じ曲線上に乗ることがわかります.
よくL/Dで話をすることがあるのは,これが原因なのでしょうか.
ためしに,切削速度に変換する形で式を書き直します.
\( V_{c} = \pi D S \)
を適用すると次式が得られます.
\( V_{c} = 30 \sqrt{ \cfrac{1}{ \cfrac{ \rho }{4} ( \cfrac{\epsilon}{ \sigma_{B}}\cfrac{L^2}{D^3} + \cfrac{32}{E}\cfrac{L^4}{D^4} ) } } \)
ルートの分母の中にLとDが含まれている項が2つあります.
\( \cfrac{\epsilon}{\sigma_{B}} \)の項はは初期条件の偏心量による影響,\( \cfrac{32}{E} \)の項は遠心力で生じる弾性変形による影響の項だと考えられます.
今回の計算条件では,\( \cfrac{\epsilon}{\sigma_{B}} \)は\( 10^{-15} \)程度の大きさで,\( \cfrac{32}{E} \)は\( 10^{-11} \)程度の大きさなので,約\( 10^4 \)倍の差があります.
その結果,\( \cfrac{L^4}{D^4} \),つまり,明らかにL/Dが含まれている\( \cfrac{32}{E}\cfrac{L^4}{D^4} \)の項のほうが優位になって,このような計算結果になったのだと考えられます.
色々計算してみましたが,結局,片持ち梁の先端集中質量として計算しているので厳密な計算ではありません.
また,破壊しない回転数がわかったとしても,遠心力による変位が大きいと穴はまともにあかないので,下穴なしで穴があけられるようなものではないです.
そのため,実際に使える回転数範囲は,上図よりももっと狭いと思います.
戻る