切削加工の専門書と論文のリストとオススメ
最終更新日：2023年07月23日

多段段付き片持ち梁の剛性

切削工具を想定して，片持ち梁先端に半径方向に荷重が作用するときの剛性計算をすると役に立つことがあります．
しかしながら，段付きの数が増えたパターンでの計算式が調べても出てこないので作りました．
条件としては片持ち梁の先端に対して半径方向に先端集中荷重を加える条件で，片持ち梁先端の変位を計算しています．

段数：1段（単純片持ち梁）
\( d = - \cfrac{L_{1}^3}{3 E_{1} I_{1}}F \)
段数：2段
\( d = ( - \cfrac{L_{12}^3}{3E_2 I_2} + \cfrac{L_{1}^3}{3E_2 I_2} - \cfrac{L_{1}^3}{3 E_{1} I_{1}})F \)
段数：3段
\( d = ( -\cfrac{L_{13}^3}{3E_3 I_3} + \cfrac{L_{12}^3}{3E_3 I_3} - \cfrac{L_{12}^3}{3E_2 I_2} + \cfrac{L_{1}^3}{3E_2 I_2} - \cfrac{L_{1}^3}{3 E_{1} I_{1}})F \)

添え字の数字は，片持ち梁の先端側からの段数を示します．
\( d \): 片持ち梁の先端変位
\( F \): 先端集中荷重
\( L_{m} \): m番目の段数の片持ち梁そのものの長さ
\( L_{mn} \): m番目の段数からn番目の段数の片持ち梁の長さの合計（\( L_{12} \)は1段目と2段目の長さの合計）
\( E_{m} \): m番目の段数のヤング率
\( I_{m} \): m番目の段数の断面二次モーメント

段数が2段までであれば，インターネット上で似たような式が出てくるので，たぶん合っていると思っています．
しかしながら，3段は調べてもあんまり出てこないと思います．
ですので，合っているのかどうかを一応調べました．

調べ方としては，FreeCADでFEMを行い，その計算結果との比較を行いました．
計算条件としては，全段の片持ち梁は丸棒を仮定しています．
先端側から直径20mm，40mmおよび50mmとして，断面二次モーメントを計算しました．
ヤング率は共通で210GPa，先端に加える荷重は1Nとしました．
各段の長さを50mmと100mmで変化させた全8条件を計算し，比較を行いました．
FEMの計算結果としては，FEM上で加える荷重と同じ方向の最大変位を全要素中から取り出して用いています．

下表に，各条件での計算結果を示します．

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	49	57
2	50	50	100	73	81
3	50	100	50	90	100
4	100	50	50	256	282
5	50	100	100	129	140
6	100	50	100	295	321
7	100	100	50	329	357
8	100	100	100	388	415

下図に両者の計算結果の比較を示します．
変位を荷重1Nでわって，剛性の逆数のコンプライアンスにしてあります．

three_stepped_bar_calculations

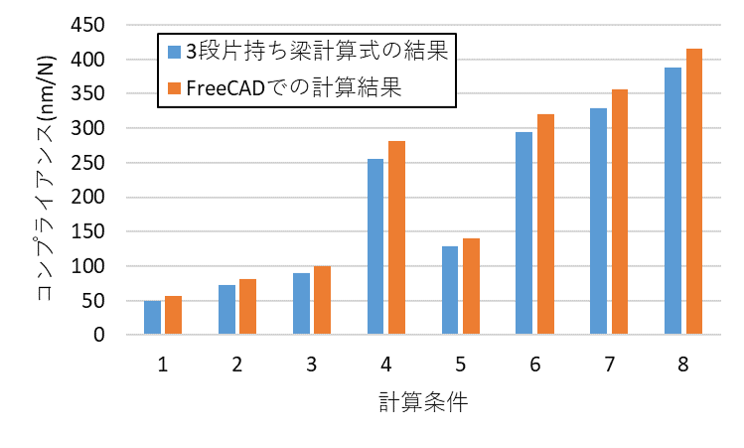
上記結果では，FreeCADでの計算結果に対して，理論式は平均で91%の値を示すことがわかりました．
この差の原因としては，FEMのメッシュ数が十分でないか，もしくは，FEMと理論式の比較であることの2つが考えられます．
FEMのメッシュ数が十分でない可能性に関しては，私の使用しているPCの性能とも関係するので，どうともならないです．
FEMと理論式の比較というのが何を言いたいのかというと，FEMで計算した場合は，理論式で考慮していない変形が生じるために理論式よりも変位が大きくなりうることを指しています．
細かく検証はしていないですが，理論式による計算結果が常に小さいのは，これが原因だと推定しています．

しかしながら，ここでは計算結果の正確性を論ずるよりは，理論式による計算結果がFEMの計算結果に対して，ここまで追従できているという点に意味を見出すべきだと考えます．
つまり，この数式を使えば3段段付き片持ち梁の剛性がある程度の精度で計算できることをうまく使うべきです．

あと，1段から3段までの式を見比べると気づくと思いますが，法則が単純に見えるので4段や5段への拡張ができるのではないかと思います．
具体的には，次式のような形になるのではないかと考えます．
数式を全部組み立てて4段以上を解くのは非常に手間がかかるので，もし拡張ができるのであれば楽だと思います．

段数：\( m \)段（\( m \geqq 2 \)）
\(\displaystyle d = \lbrack \sum_{i=2}^{m} \lbrace - \cfrac{L_{1i}^3}{3E_i I_i} + \cfrac{L_{1(i-1)}^3}{3E_i I_i} \rbrace - \cfrac{L_{1}^3}{3 E_{1} I_{1}} \rbrack F \)

ということで，4段の計算式を作ってみますと次式が得られ，上記法則と同じ形状になることが確認できました．
段数：4段
\( d = ( -\cfrac{L_{14}^3}{3E_4 I_4} + \cfrac{L_{13}^3}{3E_4 I_4} -\cfrac{L_{13}^3}{3E_3 I_3} + \cfrac{L_{12}^3}{3E_3 I_3} - \cfrac{L_{12}^3}{3E_2 I_2} + \cfrac{L_{1}^3}{3E_2 I_2} - \cfrac{L_{1}^3}{3 E_{1} I_{1}})F \)

計算条件としては，全段の片持ち梁は丸棒を仮定しています．
先端側から直径20mm，40mm，50mmおよび60mmとして，断面二次モーメントを計算しました．
ヤング率は共通で210GPa，先端に加える荷重は1Nとしました．
各段の丸棒の長さを50mmと100mmで変化させた4条件での比較を下表に示します．

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （中間）	\( L_{4} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	100	79	89
2	50	50	100	50	92	102
3	50	100	50	50	109	121
4	100	50	50	50	275	305

上記結果でも，FreeCADでの計算結果に対して，理論式は平均で90%の値を示しました．
よって，3段と4段の計算式の形から考えると，m段として示した数式は使えるのではないかと考えます．

戻る

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	49	57
2	50	50	100	73	81
3	50	100	50	90	100
4	100	50	50	256	282
5	50	100	100	129	140
6	100	50	100	295	321
7	100	100	50	329	357
8	100	100	100	388	415

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （中間）	\( L_{4} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	100	79	89
2	50	50	100	50	92	102
3	50	100	50	50	109	121
4	100	50	50	50	275	305

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	49	57
2	50	50	100	73	81
3	50	100	50	90	100
4	100	50	50	256	282
5	50	100	100	129	140
6	100	50	100	295	321
7	100	100	50	329	357
8	100	100	100	388	415

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （中間）	\( L_{4} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	100	79	89
2	50	50	100	50	92	102
3	50	100	50	50	109	121
4	100	50	50	50	275	305

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	49	57
2	50	50	100	73	81
3	50	100	50	90	100
4	100	50	50	256	282
5	50	100	100	129	140
6	100	50	100	295	321
7	100	100	50	329	357
8	100	100	100	388	415

No.	\( L_{1} \) （先端側）	\( L_{2} \) （中間）	\( L_{3} \) （中間）	\( L_{4} \) （固定端側）	数式での変位(nm)	FreeCADでの変位(nm)
1	50	50	50	100	79	89
2	50	50	100	50	92	102
3	50	100	50	50	109	121
4	100	50	50	50	275	305