L/Dとジャイロファクタの関係
「回転体の固有振動数と自動調心性」において回転体の解析をしているときにジャイロファクタが出てきています.
このジャイロファクタは,ネットで検索してもいまいち出てこないので正式な単語かどうかはよくわかりませんが,次式で計算できます.
ここでは一般化されたロータで説明します.
片方の端部が固定された長さLの棒の先に,円盤がついているような形状をしているとします.
\( \gamma = \cfrac{I_{p}}{I_{1}} = \cfrac{I_{p}}{I_{d} + ML^{2}} \)
\( I_{p} \): 極慣性能率(回転軸周りの慣性モーメント)
\( I_{d} \): 横慣性能率(重心を通り,かつ,回転軸に垂直な軸周りの慣性モーメント)
\( I_{1} \): ロータの固定端を基準とした横慣性能率
\( M \): ロータ質量
\( L \): 固定端から重心までの距離
つまり,ロータの固定端を基準座標系に取った,回転軸周りの慣性モーメントと,回転軸に垂直な軸周りの慣性モーメントの比を,ジャイロファクタと呼んでいることがわかります.
このジャイロファクタは,厚みの無視できる円盤であっても\( \gamma = 2 \)にしかならないため,\( 0 \leqq \gamma \lt 2 \)の範囲しか取りえないです.
このジャイロファクタを,円柱を回転体と仮定して計算し,それをL/Dで整理します.
これにより,円柱を回転体としたときの振る舞いがある程度わかるようになるはずです.
円柱の直径を\( D \),円柱の長さを\( L \),円柱の質量を\( M \)とします.
この円柱は片持ち梁状に固定されているとします.
回転軸周りの慣性モーメント\( I_{p} \)は次式で得られます.
\( I_{p} = \cfrac{ MD^{2} }{8} \)
重心を通り,かつ,回転軸に垂直な軸周りの慣性モーメント\( I_{d} \)は次式で得られます.
\( I_{d} = \cfrac{ MD^{2} }{16} + \cfrac{ ML^{2} }{12} \)
これを片持ち梁の固定端を基準とした座標系での慣性モーメント\( I_{1} \)に置き換えます.
\( I_{1} = I_{d} + M \cfrac{L^{2}}{4} = \cfrac{ MD^{2} }{16} + \cfrac{ ML^{2} }{3} \)
これらをジャイロファクタ\( \gamma \)の式に代入すると次式が得られます.
\( \gamma = \cfrac{I_{p}}{I_{1}} = \cfrac{6}{3+16(\cfrac{L}{D})^2} \)
ジャイロファクタは,円柱の質量に関係なく,L/Dによってのみ定まる数値であることがわかります.
次に,この数式をグラフ化してみます.
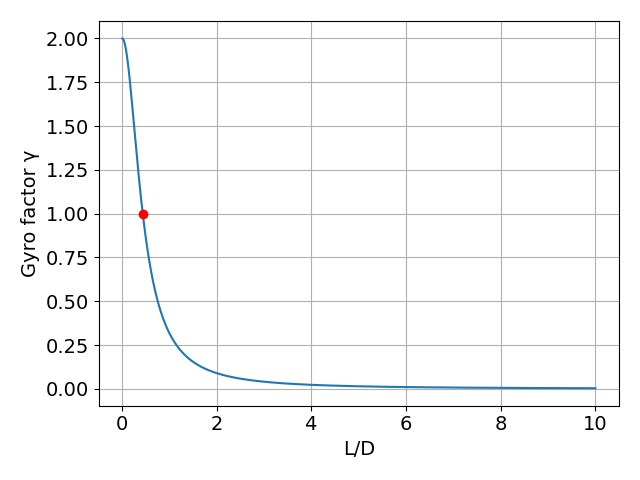
ジャイロファクタは\( 0 \leqq \gamma \lt 2 \)の範囲しか取りえず,\( \gamma = 1 \)を境として回転体の挙動が変わります.
そこで,\( \gamma = 1 \)として上式を解くと,\( \cfrac{L}{D}= \cfrac{ \sqrt{3}}{4} = 0.433 \)が得られます.
この位置は上図において赤い点で示しています.
よって,「回転体の固有振動数と自動調心性」を参照すると,L/Dが0.433以上のときは\( 0 \leqq \gamma \lt 1 \)となり,危険速度が存在することがわかります.
次に,実際に回転中の前向きと後ろ向きの固有振動数がどのように変化するかを計算します.
数式には次式を用います.
\( \omega_{f} = \lbrace \cfrac{\gamma}{2}\cfrac{\Omega}{\omega_{n}} + \sqrt{1+ (\cfrac{\gamma}{2}\cfrac{\Omega}{\omega_{n}})^{2}} \rbrace \omega_{n} \)
\( \omega_{b} = \lbrace \cfrac{\gamma}{2}\cfrac{\Omega}{\omega_{n}} - \sqrt{1+ (\cfrac{\gamma}{2}\cfrac{\Omega}{\omega_{n}})^{2}} \rbrace \omega_{n} \)
\( \omega_{f} \): 回転状態での前向き固有円振動(rad/s) \( \omega_{f} \gt 0 \)
\( \omega_{b} \): 回転状態での後ろ向き固有円振動(rad/s) \( \omega_{b} \lt 0 \)
\( \omega_{n} \): 静止状態での固有円振動(rad/s) \( \omega_{n} \gt 0 \)
\( \Omega \): 回転体の振動数(rad/s) \( \Omega \gt 0 \)
\( \gamma \): ジャイロファクタ
ただし,回転体の振動数,静止状態の固有振動数,回転中の固有振動数,ジャイロファクタと変数が多いので,ある程度の正規化を行います.
切削加工においては回転体の振動数,というのを計算するよりは,回転数(rpm)で理解したほうがわかりやすそうなので,その変更を加えます.
あと振動数をグラフ化する際にradian表記もわかりにくいので,Hz表記に変換します.
\( M_{f} = \cfrac{f_{f}}{f_{n}} = \cfrac{60\gamma}{2}\cfrac{S}{f_{n}} + \sqrt{1+ (\cfrac{60\gamma}{2}\cfrac{S}{f_{n}})^{2}} \)
\( M_{b} = \cfrac{f_{b}}{f_{n}} = \cfrac{60\gamma}{2}\cfrac{S}{f_{n}} - \sqrt{1+ (\cfrac{60\gamma}{2}\cfrac{S}{f_{n}})^{2}} \)
\( f=60S \)
\( M_{f} \): 回転状態での前向き固有振動(Hz)と静止状態での固有振動数\( f_{n} \)の比
\( M_{b} \): 回転状態での後ろ向き固有振動(Hz)と静止状態での固有振動数\( f_{n} \)の比
\( f_{f} \): 回転状態での前向き固有振動(Hz) \( f_{f} \gt 0 \)
\( f_{b} \): 回転状態での後ろ向き固有振動(Hz) \( f_{b} \lt 0 \)
\( f_{n} \): 静止状態での固有振動(Hz) \(f \gt 0 \)
\( \Omega \): 回転体の振動数(Hz) \( f \gt 0 \)
\( S \): 回転体の回転数(rpm) \( S \gt 0 \)
\( \gamma \): ジャイロファクタ
ここでは,変数を\( \cfrac{S}{f_{n}} \)として正規化します.
回転体の静止状態での固有振動数(Hz)で回転数(rpm)を割る,という特殊な正規化ですが,実用上は使いやすいかと考えます.
下図に,縦軸に\( M_{f} \)と\( M_{b} \)の絶対値を取り,横軸に\( \cfrac{S}{f_{n}} \)(rpm/Hz)をとった計算結果を示します.
ジャイロファクタは,0.5,1.0,5.0,10.0の4条件にしています.
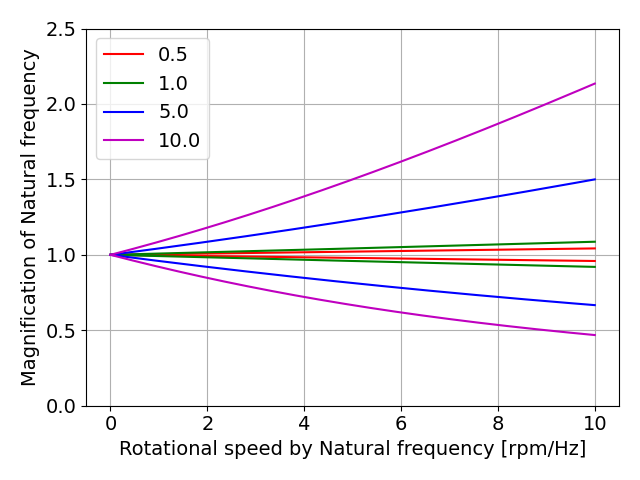
この図をどのように理解するか,の具体例を示します.
例えば,ジャイロファクタが10で静止状態での固有振動数が500Hzの回転体があったとき,それを3000rpmで回転させると,\( \cfrac{S}{f_{n}} \)は6.0になります.
このとき\( M_{f} \)が約1.62となっているため, 回転状態での前向き固有振動\( f_{f} \)は810Hzになると読み取れます.
回転体が円柱の場合,L/Dが0.433以上であればジャイロファクタは1未満となることを考慮すると,切削加工においてはジャイロファクタは1未満だと推定できます.
よって,上図より,静止状態での固有振動数(Hz)の10倍の回転数(rpm)で回したとしても,回転状態での固有振動数は大きく変化したとしてもせいぜい±約9%しか変化しないことがわかります.
参考文献:
・松下修己,田中正人,神吉博,小林正生,回転機械の振動 実用的振動解析の基本,コロナ社
・石田幸男,池田隆,回転体力学の基礎と制振,コロナ社