傾斜切削における傾斜角がすくい角に与える影響
二次元上で考えた切削をそのまま三次元に持ってきたような切削が二次元切削(Orthogonal cutting)です.
二次元切削では奥行き方向が一定になっています.
ここで,奥行き方向で傾きを追加した切削が傾斜切削(Oblique cutting)です.
傾斜切削は二次元切削と三次元の切削のはざまのような位置づけにあるので,よく使われるモデルです.
このモデルにおける「奥行き方向の傾き」が傾斜角となります.
傾斜角は,旋削では切れ刃傾き角,転削ではねじれ角(リード角)に相当します.
傾斜角を付けると,すくい角が大きくなり,切れ味が良くなります.
類似の例としては以下の2例があります.
- 包丁をただ押し付けるより,引きながら押し付けたほうが切れ味が良くなる.
- 坂の傾斜に対して真っすぐ上るより,坂の傾斜に対して斜めに上ったほうが上りやすい.
傾斜角と真のすくい角の関係性を調査することで,切れ刃傾き角やねじれ角がすくい角に与える影響,ひいては,切削抵抗に与える影響を調べることができます.
まず,すくい角と傾斜角から真のすくい角を算出する式を作成します.
\( \theta_{true} = \cfrac{\pi}{2} - \arctan \lbrace \tan(\cfrac{\pi}{2} - \theta_{rake})\cos(\theta_{oblique}) \rbrace \)
\( \theta_{true} \): 真のすくい角
\( \theta_{rake} \): すくい角
\( \theta_{oblique} \): 傾斜角
*すくい角が負のときは,数式を変更する必要があります.
すくい角を10度,20度,30度とし,傾斜角を0度から60度に変化させたときの真のすくい角を計算してみます.
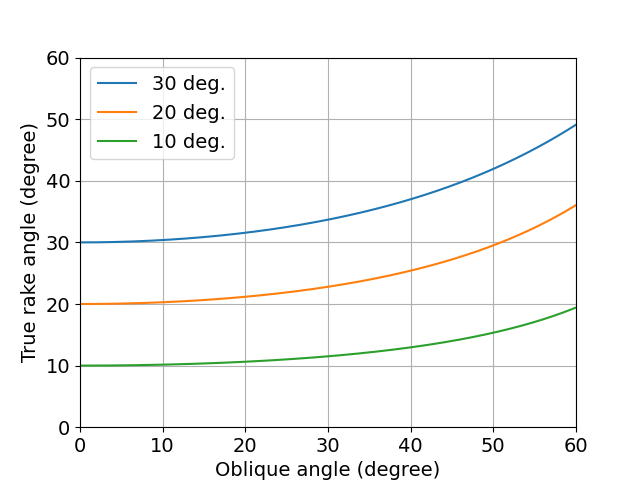
図 傾斜角と真のすくい角
傾斜角が大きくなるにつれて,真のすくい角も大きくなっていることがわかります.
また,その効果は,すくい角が大きいほどに大きいです.
この効果は,傾斜角を増やすことで,すくい角を大きくとっているのと同じ効果が得られることを示しています.
では,傾斜角1度は,真のすくい角の何度に相当するのでしょうか.
ここでは,それを調べるために上図を微分した値でグラフを作成します.
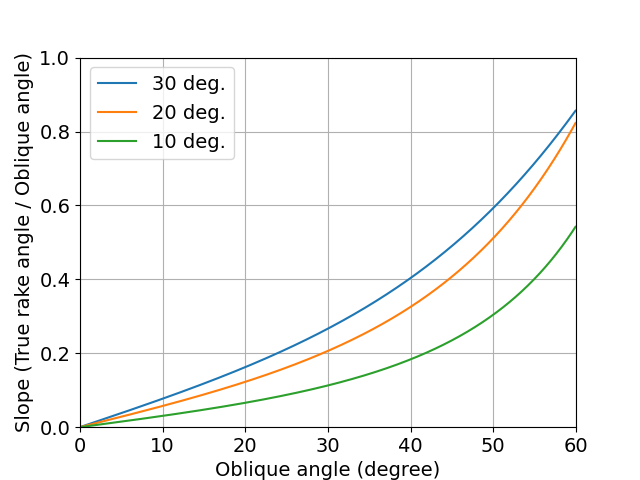
図 傾斜角と真のすくい角の微分値
すくい角30度,傾斜角40度では,0.4という値を示しています.
これは,ここから傾斜角を1度変化させると,真のすくい角が0.4度変化するのと同じ効果が得られることを示しています.
「すくい角が切削抵抗に与える影響の定量評価」で調べた結果では,すくい角1度は切削抵抗を1%変化させます.
よって,この場合,傾斜角1度は切削抵抗を0.4%変化させる可能性があります.