比切削抵抗の利用について
比切削抵抗のデータが,三菱マテリアルさんのサイトで公開されています.
私も計算するときには,大体,ここを参考に使わせてもらっています.
ここに記載がないものについてはJ-STAGEで論文を「(材質名)+比切削抵抗」で検索し,目的の比切削抵抗が記載されているものを探します.
そういった論文へのリンクは「比切削抵抗のデータベース集」にまとめました.
ただし,比切削抵抗は,刃先形状や切削条件の影響を受けるので,ここに記載されている数値が絶対的に正しいとは思わないことが重要です.
例えば,記載されている表の中でも,一刃あたり送り量によって,比切削抵抗が変わっています.
これは,刃先丸みや,材質の寸法効果(温度や,欠陥の存在確率)が影響しているためです.
他にも,切削速度によっても切削抵抗は変わりますし,材質が同じでも硬度が違うと比切削抵抗は変わるはずです.
ただし,アルミと鋼で比切削抵抗が大きく異なる,といった傾向が覆るまでの変化は生じないはずです.
ですので,あくまでも目安だと思って使うのが正しいです.
三菱マテリアルさんのサイトで紹介されている比切削抵抗は切削面積に比例することになっていますが,これとは別な比切削抵抗の定義もあります.
それは,切れ刃長さと切削面積に切削抵抗が比例すると考える比切削抵抗であり,2個の定数を1セットとして使い,切削抵抗との関係を示します.
切れ刃長さに比例する項目は,刃先丸みの影響と,逃げ面摩擦の影響を考慮する.
切削面積に比例する項目は,せん断面の影響と,すくい面摩擦の影響を考慮する.
ということになっているはずなので,結構理にかなっていると思います.
しかも,その数式を使うと,一刃あたり送り量によって比切削抵抗が大きく変化する影響も考慮することができます.
以下に,数式を記載しておきますが,詳細に興味があれば調べてみてください.
私は,何にそれが載っていたのかを失念してしまっているので,どこでこれを覚えたのかわかりません.
参考例としては,「傾斜切削理論に基づくエンドミル加工の切削力モデル」があります.
この論文中の式2では,同じような数式が使われています.
\( F_{c} = Ka_{p}f_{z} \):切削面積にのみ切削抵抗が比例するモデル
\( F_{c} = K_{a}a_{p}f_{z} + K_{p}a_{p} \):切削面積と切れ刃長さに切削抵抗が比例するモデル(Mechanistic force model)
\( F_{c} \):切削抵抗
\( K \):比切削抵抗
\( a_{p} \):軸方向切込み量
\( f_{z} \):一刃当たりの送り量
\( K_{a} \):切削面積に比例する比切削抵抗
\( K_{p} \):切れ刃長さに比例する比切削抵抗
上記2式を組み合わせると次式のようになります.
\( Ka_{p}f_{z} = K_{a}a_{p}f_{z} + K_{p}a_{p} \)
両辺を\( a_{p}f_{z} \)で割ると,次式が得られます.
\(\displaystyle K = K_{a} + \cfrac{K_{p}}{f_{z}} \)
よって,2つの比切削抵抗のモデルで表すことにより,\( f_{z} \)が小さくなると,従来の単一の比切削抵抗で値が大きくなる効果が記述できていることがわかります.
下図は,いくつかの比切削抵抗のデータと,それらのデータに最小二乗法を適用し,切削面積と切れ刃長さに切削抵抗が比例するモデルの係数を計算して作図した結果を示します.
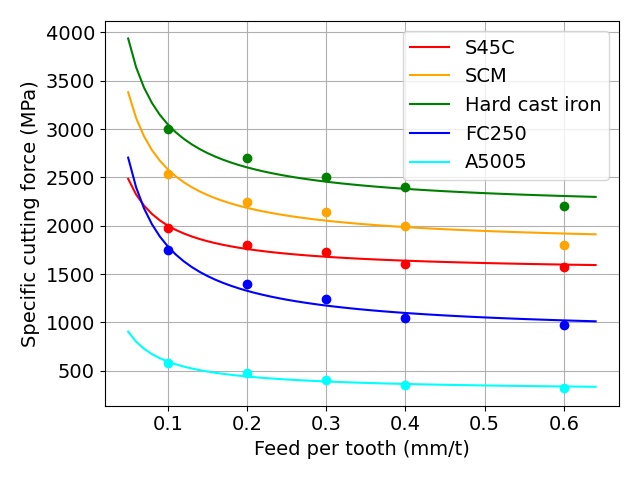
図 1刃当たりの送り量と比切削抵抗の関係
各被削材において同定した2種の係数を以下に示します.
| 被削材 | \( K_{a} \) (N/mm2) | \( K_{p} \) (N/mm) |
|---|---|---|
| S45C | 1518.3 | 48.4 |
| SCM | 1787.3 | 79.7 |
| Hard cast iron | 2160.1 | 88.9 |
| FC250 | 868.8 | 91.8 |
| A5005 | 286.9 | 30.9 |
ただ,この数式表現がベストかというと,そうでもないと考えます.
「丸みのある切れ刃に作用する切削抵抗 : 第1報, 切削抵抗に関する基礎的な検討」には,いくつかの切削抵抗測定結果への数式のフィッティング結果が記載されています.
大体,切り取り厚さのべき乗で比切削抵抗が表現されています.
これはKienzle force modelという近似式です.
よって,どの数式を使っても,参考程度に考えておくのがいいのではないでしょうか.
せっかくなので,ここでもひとつ試してみることにします.
それは-0.22のべき乗を用いて比切削抵抗を表現するモデルです.
「切削加工技術者のための知識と理論」の270ページでも,このモデルが使われています.
\( K_{exp} = \alpha f_{z}^{-0.22} \)
\( K_{exp} \):比切削抵抗
\( \alpha \):係数
下図に,べき乗モデルを使って,一刃当たりの送り量による比切削抵抗の変化をフィッティングした結果を示します.
実線はべき乗モデルでの計算結果を示しています.
比較のために,先ほど計算した2つの比切削抵抗を用いるモデルでの計算結果を破線で追記しています.
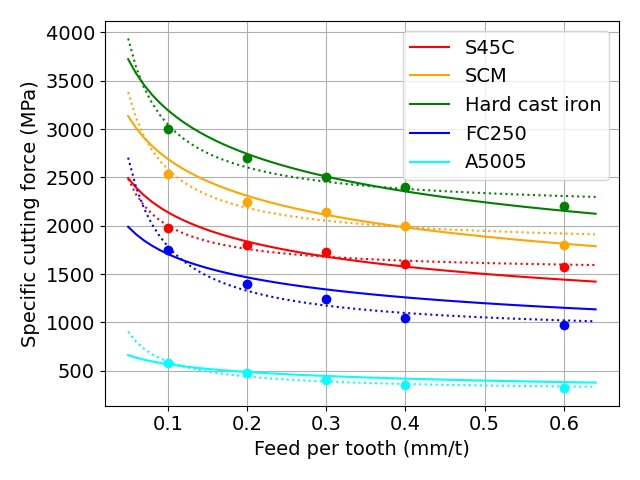
図 1刃当たりの送り量と比切削抵抗の関係
各被削材において同定した係数を以下に示します.
| 被削材 | \(\alpha \) |
|---|---|
| S45C | 1289.8 |
| SCM | 1621.7 |
| Hard cast iron | 1926.1 |
| FC250 | 1029.6 |
| A5005 | 342.7 |
2つの比切削抵抗を用いるモデルでは,一刃当たりの送り量が小さくなったときに大小関係が逆転する場合がありました.
べき乗モデルでは,それがないので,被削材ごとの大小関係が逆転しにくくなっているようにみえます.
その反面,計算のもとになっている入力値にあまり追従していないようにみえます.
参考までに,下図に,切込み量を1mmに設定した場合の切削抵抗の計算結果を示します.
実線はべき乗モデルでの計算結果,破線は2つの比切削抵抗を用いるモデルでの計算結果を示します.
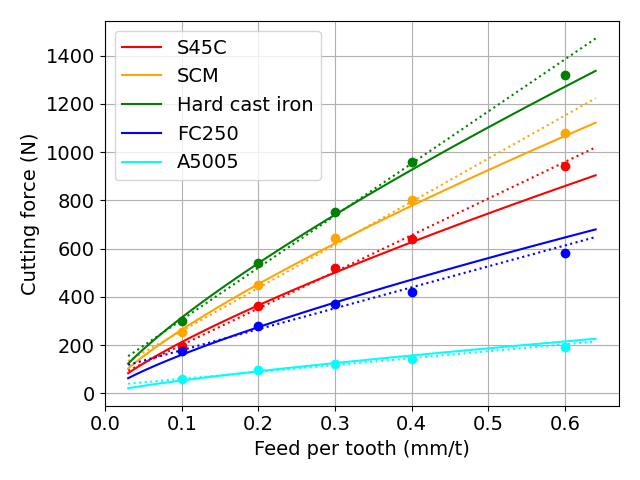
図 比切削抵抗からの切削抵抗の算出結果
べき乗モデルでの計算結果を見ていて,近似式の形自体がいまいち良くないように思いました.
近似式の種類にも書きましたが,べき乗の良いところは近似式の形の融通が利きやすい点にあります.
そこで,べき乗の係数自体も近似してみることにします.
\( K_{exp2} = \alpha f_{z}^{\beta} \)
\( K_{exp} \):比切削抵抗
\( \alpha \):係数
\( \beta \):係数
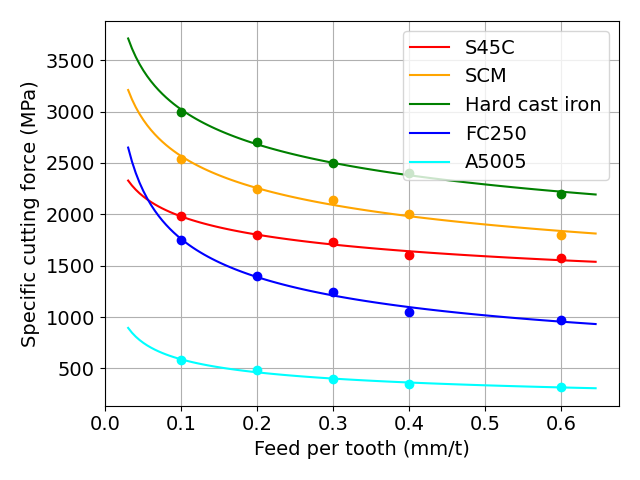
図 1刃当たりの送り量と比切削抵抗の関係
| 被削材 | \(\alpha \) | \(\beta \) |
|---|---|---|
| S45C | 1449.3 | -0.135 |
| SCM | 1670.8 | -0.186 |
| Hard cast iron | 2034.0 | -0.171 |
| FC250 | 802.8 | -0.341 |
| A5005 | 263.8 | -0.348 |
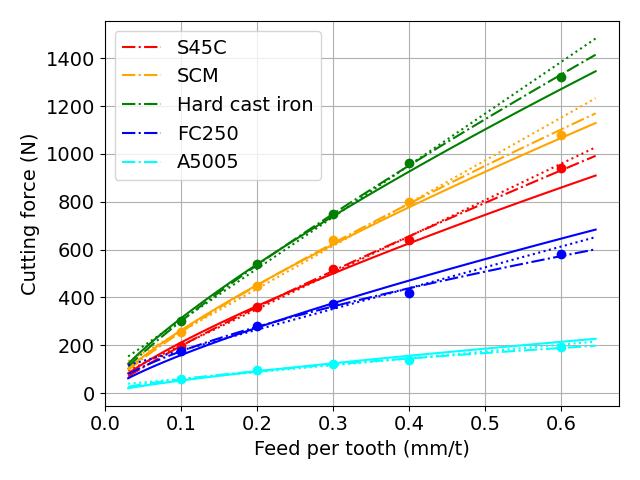
図 比切削抵抗からの切削抵抗の算出結果
*一点鎖線が変数2つを近似したべき乗モデル
結果としては,係数βは-0.22から異なる値になっていて,それによって近似式の形は元データに沿う形になりました.
比切削抵抗の近似にべき乗を使うのであれば,この形で使うのが良いと思います.
戻る