旋削加工での表面粗さRaとRzの理論計算式(計算機能あり)
まず,以下に表面粗さのパラメータである算術平均粗さRaと最大高さRzを試算する部位を示します.
旋削工具の刃先の丸コーナ部のみにて加工面が形成される場合を想定しています.
計算機能の実装にJavaScriptを使用しているので,必要に応じてJavaScriptをONにしてください.
計算方法には触れませんが,数値計算解および二乗平均平方根高さRq,二乗平均平方根傾斜Rdq,スキューネスRsk,クルトーシスRkuも算出できます.
刃先の丸コーナのコーナ半径(mm):
1回転あたりの送り量(mm/rev):
| 面粗さ | 厳密解 | 近似解 | 数値計算解 |
|---|---|---|---|
| Ra (μm) | |||
| Rz (μm) | |||
| Rq (μm) | |||
| Rdq | |||
| Rsk | |||
| Rku |
*1回転あたりの送り量による面粗さの変化を示すグラフを見たい場合は「旋削加工での表面粗さのグラフ作成(計算機能あり)」でご確認ください.
以下では,各数値の計算式や,厳密解と近似解との差異などについて記載しています.
旋削加工において,刃先先端の丸コーナで加工面を形成したとき,丸コーナの円弧が加工面に転写されます.
この加工面の表面粗さRzの近似解が次式で得られることは有名です.
\( R_{z} = \cfrac{ f_{z}^2 }{8R} \)
\( f_{z} \): 1回転あたりの送り量
\( R \): 丸コーナのコーナ半径
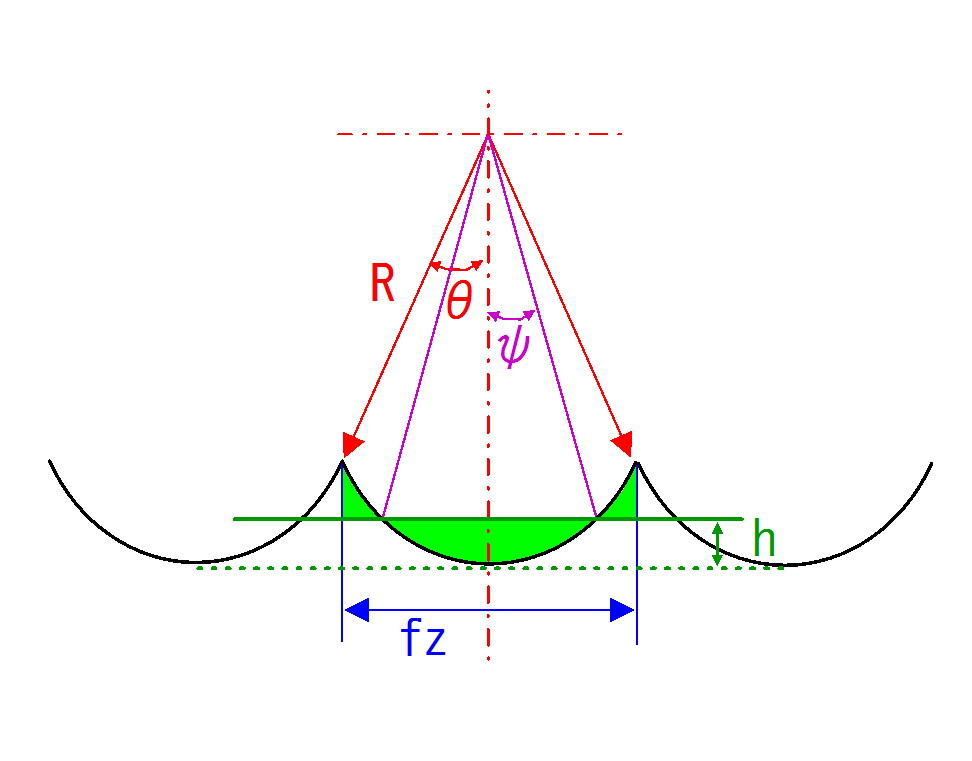
図 旋削加工面の模式図
では,表面粗さRaは,どうすれば得られるのでしょうか.
また「Raの4倍くらいがRz」と言われていますが,実際のところはどうなのでしょうか.
ここでは,そのあたりを調べます.
まず,Raの厳密解の計算式を作ります.
作ってみてわかったのですが,Rzの計算式ほど簡単ではありません.
導出過程の詳細は,ページ下部のおまけ4に示しています.
\( \theta = \arcsin ( \cfrac{ f_{z} }{2R} ) \)
\( h = R \lbrace \cfrac{ 2\sin(\theta) - \sin(\theta)\cos(\theta) - \theta }{2\sin(\theta)} \rbrace \)
\( \psi = \arccos ( \cfrac{ R - h }{R} ) \)
\( R_{a} = R \lbrace \cfrac{ \psi - \sin(\psi)\cos(\psi) }{\sin(\theta)} \rbrace \)
hは,Raを算出するときに使う平均線の位置を示しています.
平均線から上側の面積と下側の面積が同じになります.
ついでに,Rzの近似解との比較のために,Rzの厳密解も算出しておきます.
\( R_{z} = R - R \cos(\theta) \)
次に,作った計算式でRaの厳密解、Rzの近似解、およびRzの厳密解を計算します.
丸コーナのコーナ半径を0.2mm,0.4mm,0.8mm,1.6mmとします.
1回転あたりの送り量は,各コーナ半径において,その2倍の値までとります.
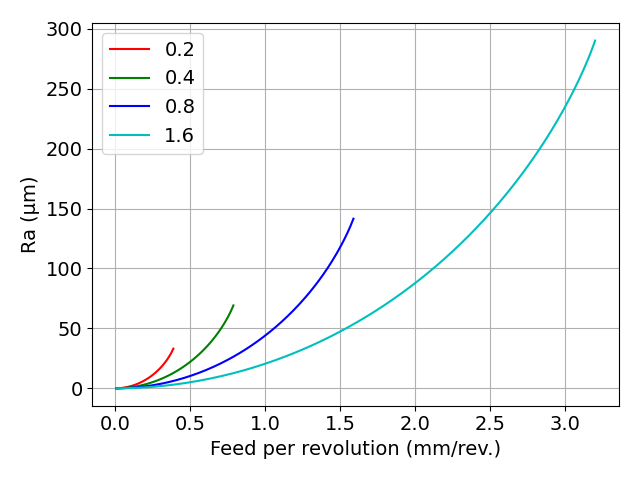
図 Raの厳密解(各コーナ半径の2倍の送り量まで計算)
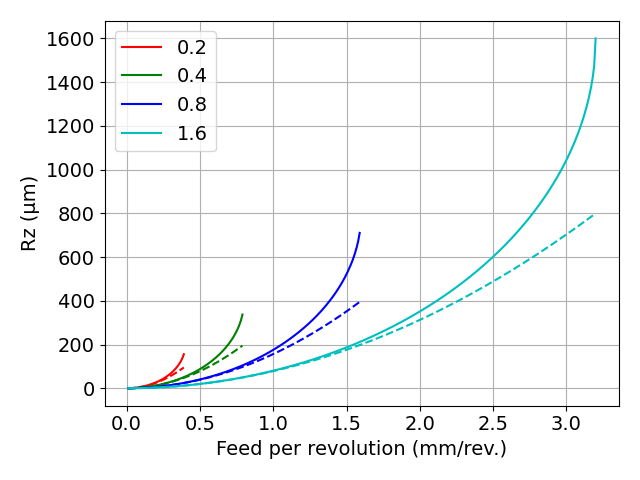
図 Rzの近似解と、Rzの厳密解(各コーナ半径の2倍の送り量まで計算)
実線は厳密解を,破線は近似解を示します.
1回転あたりの送り量が大きくなるにつれ,厳密解と近似解の差が大きくなっていることがわかります.
上記計算結果を使って,Rz/Raを計算し,比を求めます.
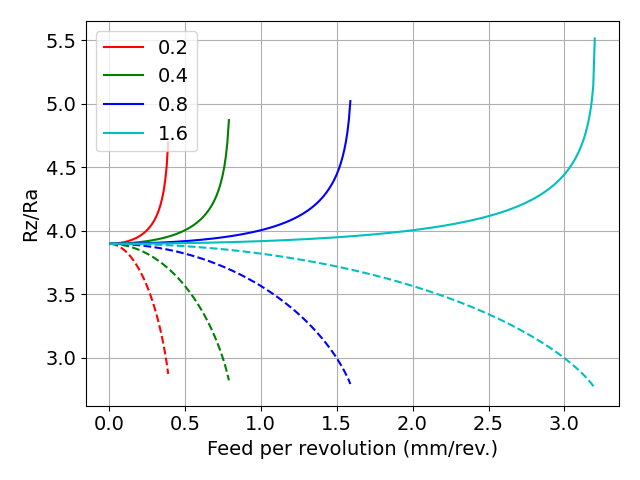
図 Rz/Raの計算結果(各コーナ半径の2倍の送り量まで計算)
実線はRzの厳密解を用いた計算結果,破線はRzの近似解を用いた計算結果を示します.
1回転あたりの送り量が大きくなるにつれ,どちらの計算結果でも4から離れていくことがわかります.
1回転あたりの送り量が大きくなったときのずれ量が大きく,詳細がわかりにくいため,計算条件を狭くします.
具体的には,1回転あたりの送り量は,各コーナ半径において,その1倍の値までとることにして再計算します.
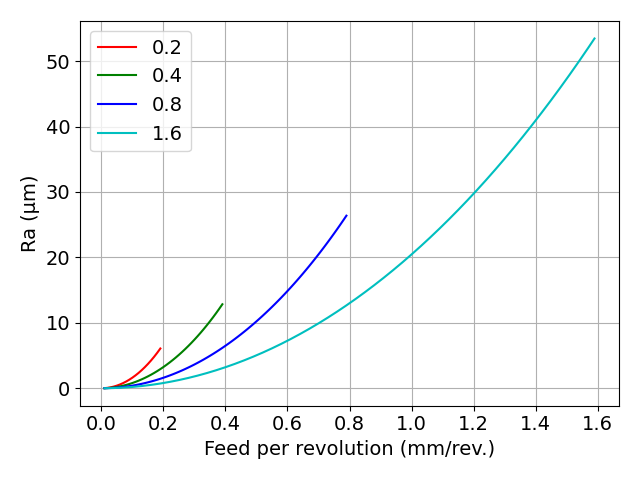
図 Raの厳密解(各コーナ半径の1倍の送り量まで計算)
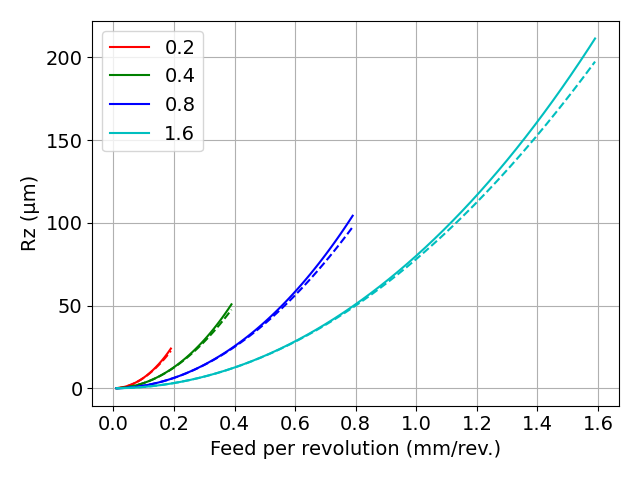
図 Rzの近似解と、Rzの厳密解(各コーナ半径の1倍の送り量まで計算)
実線は厳密解を,破線は近似解を示します.
今回の計算範囲であれば,両計算結果はほぼ同等といえます.
上記計算結果を用いてRz/Raを計算して比を求めます.
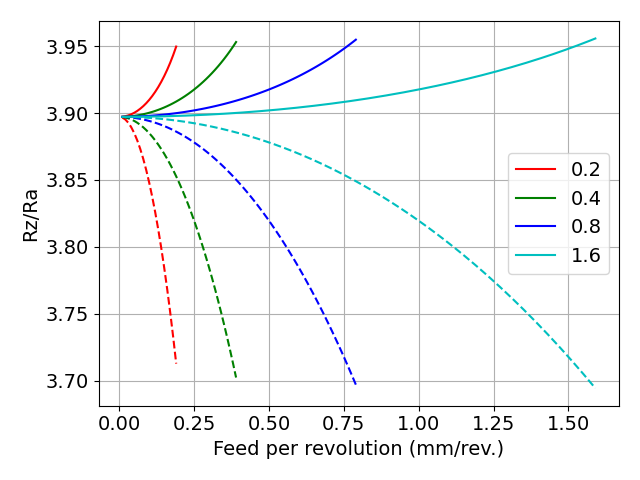
図 Rz/Raの計算結果(各コーナ半径の1倍の送り量まで計算)
実線はRzの厳密解を用いた計算結果,破線はRzの近似解を用いた計算結果を示します.
Rzの厳密解を用いた場合は,3.90から3.95の比となっています.
Rzの近似解を用いた場合は,3.70から3.90の比となっています.
よって,「Rz/Raが4になる」といわれているのは,ここからきていることがわかります.
しかしながら,今回の計算結果から,3.9を使ったほうが実際の計算結果に近いと考えます.
ただし,計算どおりの面粗さが実際の切削加工において得られることは少ないので,計算結果を過信しないほうがいいと思います.
おまけ1:Rzの近似解の導出
\( R_{z} = R - R \cos(\theta) \)
\( = R - R \cfrac{ \sqrt{R^2 - (f_{z}/2)^2} }{R} \)
\( = R - R \sqrt{ 1 - ( \cfrac{f_{z}}{2R} )^2} \)
ここで,\( \sqrt{ 1 -x } = (1-x)^{0.5} \approx 1 - \cfrac{1}{2}x \) の近似を適用します.
\( R_{z} \approx R - R \lbrace 1 - \cfrac{1}{2} ( \cfrac{f_{z}}{2R} )^2 \rbrace \)
\( = R - R + \cfrac{R}{2} ( \cfrac{f_{z}}{2R} )^2 \)
\( = \cfrac{f_{z}^2 }{8R} \)
おまけ2:三角波形状でのRzとRaの厳密解
三角波の両端の角度を\( \alpha \),\( \beta \)とすると,次式が得られます.
\( R_{z} = \cfrac{\tan(\alpha)\tan(\beta)}{\tan(\alpha) + \tan(\beta)}f_{z} \)
\( R_{a} = \cfrac{ R_{z} }{4} \)
\( h = \cfrac{ R_{z} }{2} \)
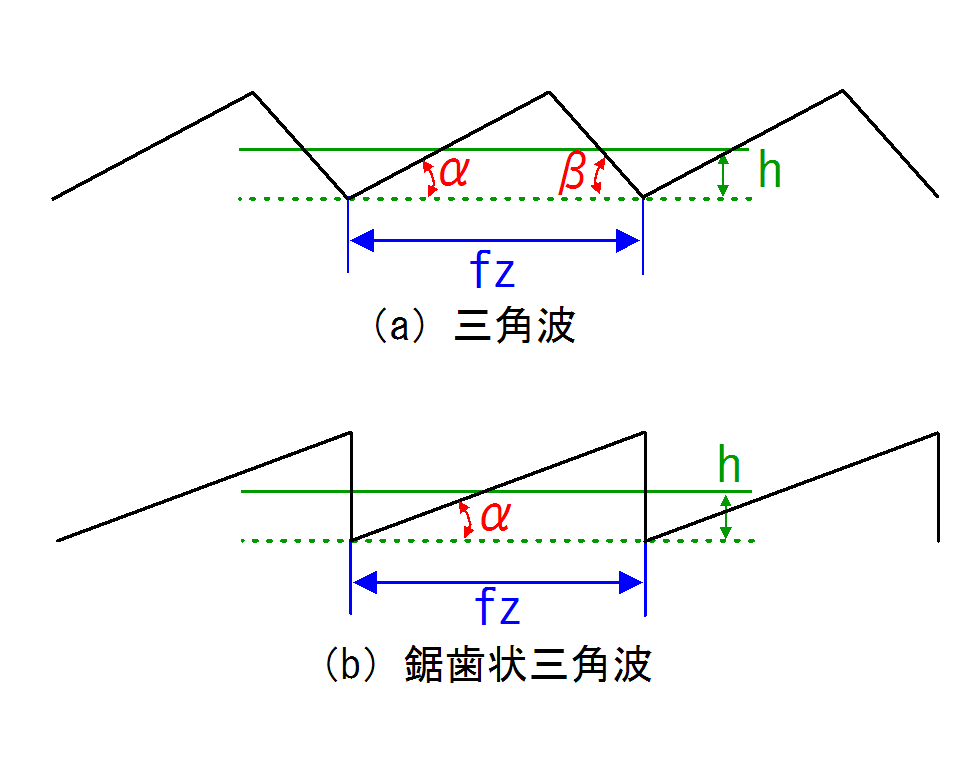
もし,三角波の形状が二等辺三角形であった場合,\( \alpha = \beta \)となるので,
\( R_{z} = \cfrac{\tan(\alpha)}{2}f_{z} \)
\( R_{a} = \cfrac{ R_{z} }{4} \)
となります.
また,三角波が鋸歯状であった場合,\( \alpha = \cfrac{\pi}{2} \)または\( \beta = \cfrac{\pi}{2} \)という条件になります.
今回は,\( \beta = \cfrac{\pi}{2} \)であるとします.
\( R_{z} = \cfrac{\tan(\alpha)}{\cfrac{\tan(\alpha)}{\tan(\beta)}+1}f_{z} \)
と書き換えたうえで,
\( \lim_{\beta \to \cfrac{\pi}{2}} \tan(\beta) = \infty \)
を考慮すると,
\( R_{z} = \tan(\alpha)f_{z} \)
\( R_{a} = \cfrac{ R_{z} }{4} \)
となります.
三角波だと「Raの4倍がRz」が常に成立することがわかります.
もしかすると、コーナ半径で生成される円弧形状の加工面でも4倍だと言われているのは,三角波での数値をそのまま使っているだけなのかもしれません.
おまけ3:Raの近似解
「切削加工技術者のための知識と理論」のp.362にRaの近似式の導出が載っていることに最近気が付きました.
刃先先端の丸コーナで加工面を形成したときのRaの近似式は次式で示されます.
\( R_{a} = \cfrac{1}{ 18 \sqrt{3} }\cfrac{ f_{z}^2 }{ R } \)
下図にRaの厳密解と近似解の比較を示します.
実線はRaの厳密解を用いた計算結果,破線はRaの近似解を用いた計算結果を示します.
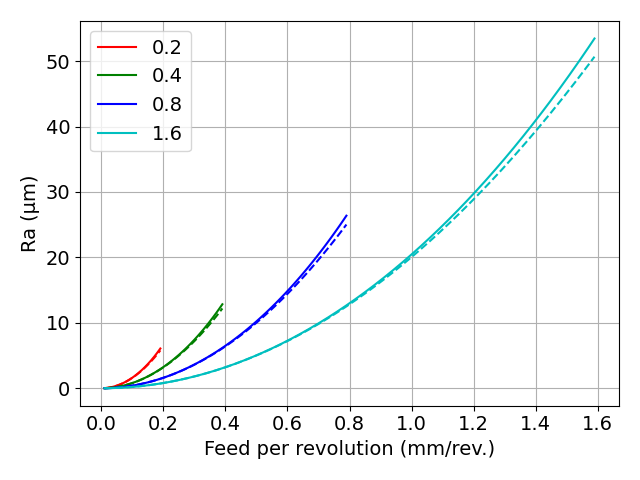
図 Raの厳密解と近似解(各コーナ半径の1倍の送り量まで計算)
大体,同じような値を示していることがわかります.
ここでRaの近似解の数式をよく見てみると,Rzの近似解\( R_{z} = \cfrac{ f_{z}^2 }{8R} \)とよく似た形をしていることがわかります.
そこで,近似式同士を用いて,Raの何倍がRzになるのかを調べます.
\( \cfrac{ R_{z} }{ R_{a} } = \cfrac{ \cfrac{ f_{z}^2 }{8R} }{ \cfrac{1}{ 18 \sqrt{3} }\cfrac{ f_{z}^2 }{ R } } = \cfrac{ 9 \sqrt{3}}{ 4 } \approx 3.90 \)
近似式同士を使うと「Raの3.90倍がRz」が常に成立することがわかります.
本ページの冒頭で厳密解の導出をしていますが,近似解でもそこまで大きく外れるわけではないので,近似解を使ったほうが簡単に計算できると思います.
というよりは,「\( R_{z} = \cfrac{ f_{z}^2 }{8R} \)」と,「Raの3.90倍がRz」の2つだけを覚えていればいいと思います.
おまけ4:Raの厳密解の導出過程
最初の段階で既知なのは\( R \)と\( f_{z} \)だけです.
\( \theta \),\( \psi \),\( h \),\( R_{a} \)の4つは未知です.

図 旋削加工面の模式図
まず,\( \theta \)を導出します.
\( R \sin \theta = \cfrac{ f_{z} }{2} \)
より,
\( \theta = \arcsin ( \cfrac{ f_{z} }{2R} ) \)
となります. 次に,\( \psi \)を導出します.
\( \psi \)は\( h \)によって値が定まります.
この段階では,\( h \)が未知なので,\( \psi \)も未知ですが,導出の関係上,先に出します.
\( R \cos \psi = R - h \)
より, \( \psi = \arccos ( \cfrac{ R - h }{R} ) \)
となります.
次に\( h \)を導出します.
半径Rの円弧の平均線が,底面からどのくらいの位置にあるか,というのを示すのが\( h \)です.
つまり,半径Rの円弧と平均線によって形成される,平均線の下側の面積Aと上側の面積Bは同じになります.
この性質を用いて導出します.
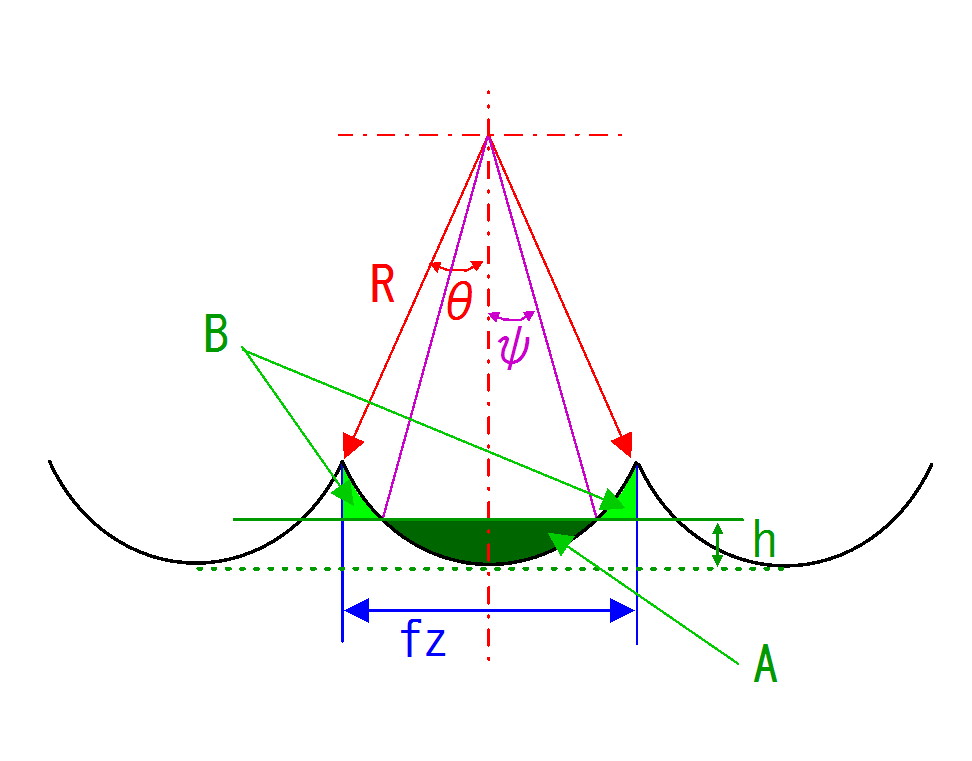
図 旋削加工面の模式図1
まず,下側の面積Aの式を立てます.
これは,半径Rで角度\( 2 \psi \)の扇形から,半径Rの中心点を頂点とした二等辺三角形の面積を引くことで得られます.
\( A = R^{2} \pi \cfrac{2 \psi}{ 2 \pi} - (R \sin \psi \cdot R \cos \psi \cdot \cfrac{1}{2}) \cdot 2 \)
\( A = R^{2} \psi - R^{2} \sin \psi \cos \psi \)
次に,面積Bの式を作ります.
まず,面積Bの求め方を示します.
面積Cから面積Aを引いたものを面積Dとします.
面積Cは面積Aと類似の数式で算出できます.
面積Eから面積Dを引けば,残りは面積Bになります.
面積Eは幅\( f_{z} \),高さ\( R - R\cos \theta - h \)の長方形の面積です.
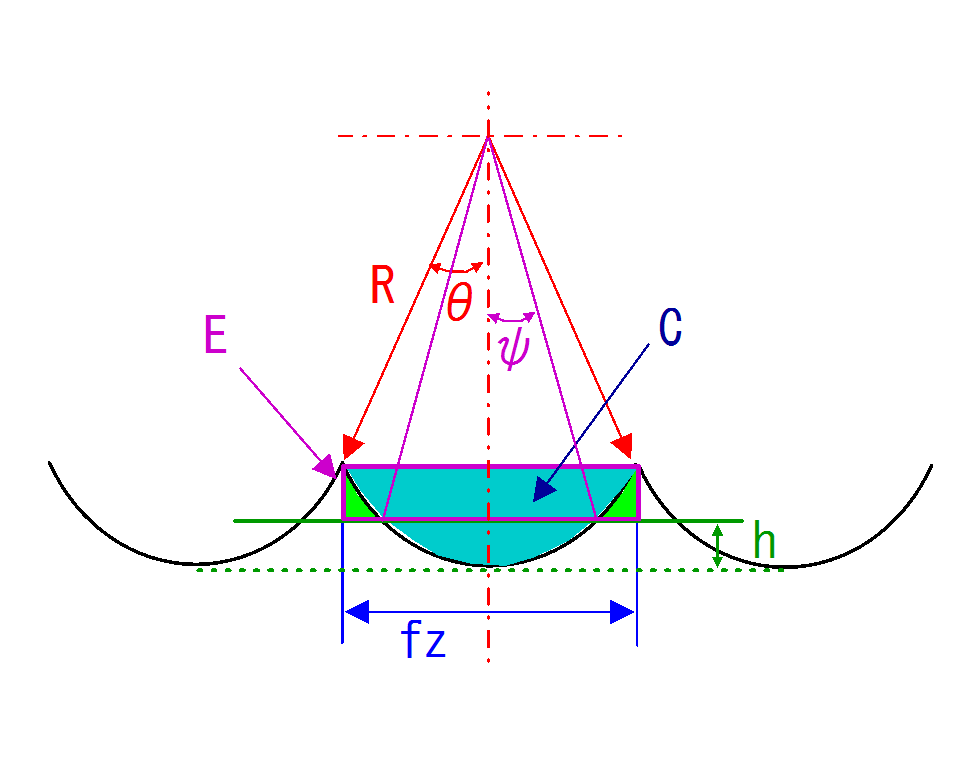
図 旋削加工面の模式図2
では,実際に面積Bの式を立てます.
まず,面積Cを導出します.
これは面積Aの頂角を\( 2 \theta \)にするだけなので次式になります.
\( C = R^{2} \theta - R^{2} \sin \theta \cos \theta \)
次は面積Dです.
\( D = C - A \)
\( D = ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) - ( R^{2} \psi - R^{2} \sin \psi \cos \psi ) \)
次は,面積Eです.
\( E = f_{z} ( R - R\cos \theta - h ) \)
最後に面積Bを導出します.
\( B = E - D \)
\( B = f_{z} ( R - R\cos \theta - h ) - \lbrace ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) - ( R^{2} \psi - R^{2} \sin \psi \cos \psi ) \rbrace \)
\( B = f_{z} ( R - R\cos \theta - h ) - ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) + ( R^{2} \psi - R^{2} \sin \psi \cos \psi ) \)
ここで面積Aと面積Bの式ができたので,これをつなぎます.
\( A = B \)
\( R^{2} \psi - R^{2} \sin \psi \cos \psi = f_{z} ( R - R\cos \theta - h ) - ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) + ( R^{2} \psi - R^{2} \sin \psi \cos \psi ) \)
左辺と,右辺第3項が同じなので,これを消去します.
\( 0 = f_{z} ( R - R\cos \theta - h ) - ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) \)
\( h \)を含む項を左辺に,残りの項を右辺に残します.
\( f_{z} h = f_{z} ( R - R\cos \theta ) - ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) \)
ここで,\( f_{z} = 2R \sin \theta \)を代入します.
\( 2Rh \sin \theta = 2R \sin \theta ( R - R\cos \theta ) - ( R^{2} \theta - R^{2} \sin \theta \cos \theta ) \)
\( 2Rh \sin \theta = 2R^{2} \sin \theta - 2R^{2} \sin \theta \cos \theta - R^{2} \theta + R^{2} \sin \theta \cos \theta \)
\( 2Rh \sin \theta = 2R^{2} \sin \theta - R^{2} \sin \theta \cos \theta - R^{2} \theta \)
\( h = \cfrac{2R^{2} \sin \theta - R^{2} \sin \theta \cos \theta - R^{2} \theta}{ 2R \sin \theta } \)
\( h = \cfrac{2R \sin \theta - R \sin \theta \cos \theta - R \theta}{ 2 \sin \theta } \)
\( h = R \lbrace \cfrac{2 \sin \theta - \sin \theta \cos \theta - \theta}{ 2 \sin \theta } \rbrace \)
これで\( h \)が導出できました.
つまり,\( \psi \)も導出できたことになります.
次に\( R_{a} \)を導出します.
\( R_{a} \)は,その定義から考えると,半径Rの円弧と平均線によって形成される上下の面積の和を,横軸の長さで割ることによって得られます.
つまり,次式で計算できます.
\( R_{a} = \cfrac{A+B}{f_{z}} \)
現時点で\( A=B \)となっているので,次式も成立します.
\( R_{a} = \cfrac{ 2A }{f_{z}} \)
ここで,\( A = R^{2} \psi - R^{2} \sin \psi \cos \psi \)と,\( f_{z} = 2R \sin \theta \)を代入します.
\( R_{a} = \cfrac{ 2( R^{2} \psi - R^{2} \sin \psi \cos \psi ) }{ 2R \sin \theta } \)
\( R_{a} = \cfrac{ R \psi - R \sin \psi \cos \psi }{ \sin \theta } \)
\( R_{a} = R \lbrace \cfrac{ \psi - \sin \psi \cos \psi }{ \sin \theta } \rbrace \)
これで\( R_{a} \)も導出できました.