旋削加工での算術平均粗さRaの計算式の比較
旋削工具のノーズR部分のみで切削した場合に生成される加工面の算術平均粗さRaの理論値を計算する数式がいくつかあります.
数式自体の複雑性が各々異なっており,その複雑性に伴って計算精度も異なっているはずですが,どのくらい違うのかはよくわかりません.
そこで,このページでは,それらの計算結果の差異を調べます.
- Raの厳密解
本WEBサイトの「旋削加工での表面粗さRaとRzの理論計算式(計算機能あり)」にて示した厳密解が次式です.
上記ページではRaの厳密解と数値計算解を両方出力しており,それが常に一致しているので,この厳密解は妥当であると判断しています.
\( \theta = \arcsin ( \cfrac{ f_{z} }{2R} ) \)
\( h = R \lbrace \cfrac{ 2\sin(\theta) - \sin(\theta)\cos(\theta) - \theta }{2\sin(\theta)} \rbrace \)
\( \psi = \arccos ( \cfrac{ R - h }{R} ) \)
\( R_{a} = R \lbrace \cfrac{ \psi - \sin(\psi)\cos(\psi) }{\sin(\theta)} \rbrace \)
- Ra近似解1
「切削加工技術者のための知識と理論」のp.362に記載されているRaの近似式が次式です.
\( R_{a} = \cfrac{1}{ 18 \sqrt{3} }\cfrac{ f_{z}^2 }{ R } \)
- Ra近似解2
「J-E. Ståhl, F. Schultheiss, S. Hägglund, Analytical and Experimental Determination of the Ra Surface Roughness during Turning, Procedia Engineering, Volume19, 2011, pp.349-356」の式8にRaの近似解の計算式が記載されています.
この式8では,Raの2段階の近似が行われていますので,式8の真ん中部分を抜き出したものが次式です.
\( R_{a} = 0.77 \cdot \left[ R - \cfrac{R^2}{f_{z}} \arcsin( \cfrac{f_{z}}{2R} ) - \cfrac{R}{2} \sqrt{ 1-\cfrac{f_{z}^2}{4R^2} } \right] \)
given that \( f_{z} \le 2\sqrt{a_{p} (2R - a_{p}) } \le 2R \)
ただし,当該論文中の式5と式8を見比べると,式5ではルート内の分母にあるRが二乗されていますが,式8では二乗されていないです.
近似の過程で数式が変化するのかとも考えたのですが,両式の計算結果を確認したところ,これは単純な記載ミスのようです.
論文中の式8が間違っており,ルート内の分母にあるRが二乗されているほうが正しいので,上式に示す式8では当該部分を修正しています.
- Ra近似解3
Ra近似解2で示した論文の式8の右端の部分を抜き出したものが次式です.
\( R_{a} = 0.77R \cdot \left( 1- \cfrac{ \cfrac{f_{z}}{2R} }{ \arcsin( \cfrac{f_{z}}{2R} ) } \right) \)
given that \( f_{z} \le 2\sqrt{a_{p} (2R - a_{p}) } \le 2R \)
\( f_{z} \): 1回転当たりの送り量
\( R \): ノーズR(半径)
\( a_{p} \): 切込み深さ
ノーズRを0.2mm,0.4mm,0.8mm,1.6mmと変化させ,それぞれにおいて,1回転あたりの送り量\( f_{z} \)をノーズR分だけ変化させます.
上記計算条件下におけるRaの計算結果をグラフにして厳密解と近似解を比較します.
- 厳密解と近似解1
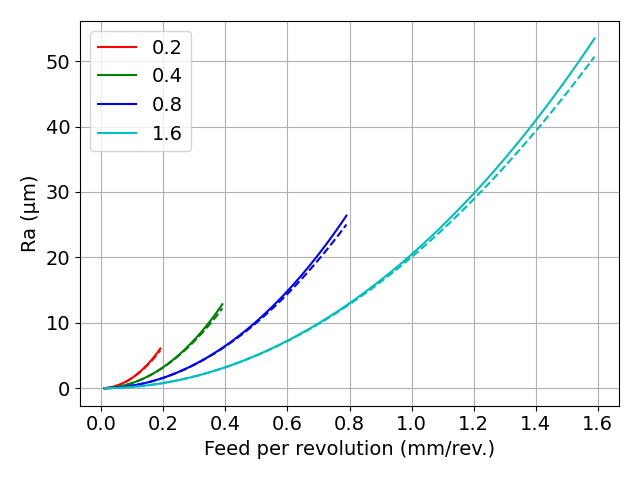
実線が厳密解,破線が近似解
- 厳密解と近似解2
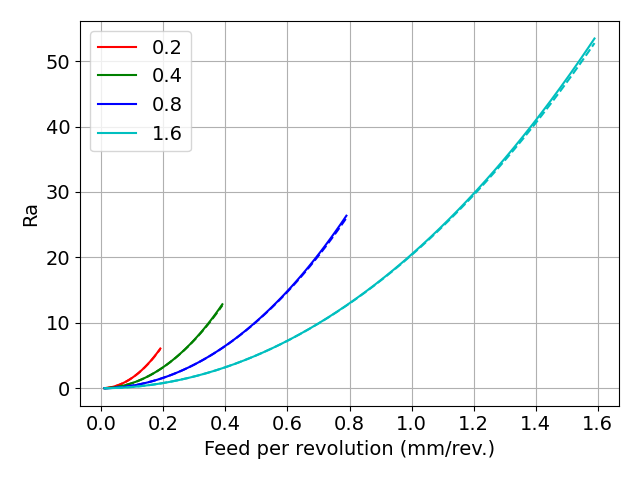
実線が厳密解,破線が近似解
- 厳密解と近似解3
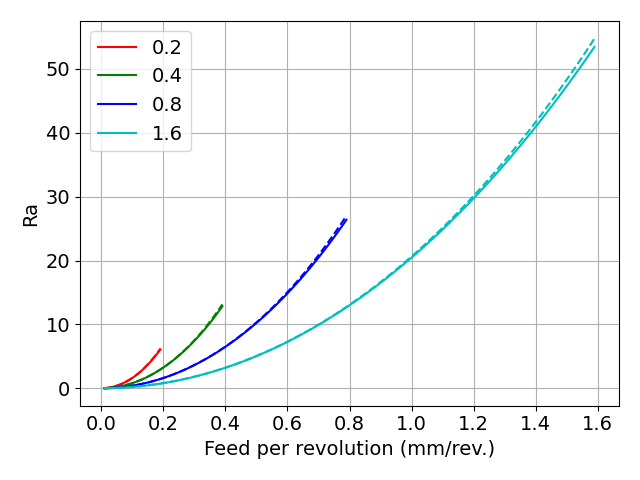
実線が厳密解,破線が近似解
では,この「それなりに」というのを定量的に評価するために,近似解/厳密解を計算し,グラフ化します.
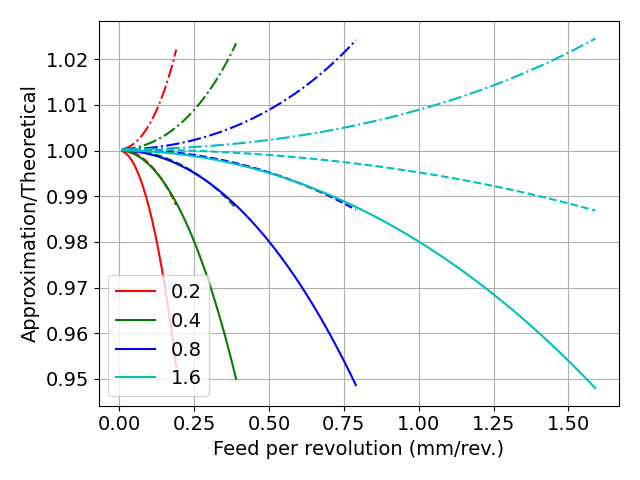
実線が近似解1/厳密解,破線が近似解2/厳密解,1点鎖線が近似解3/厳密解
縦軸が1のとき,厳密解と近似解が一致しているということを示す.
近似解2(最大誤差約1%)<近似解3(最大誤差約2%)<近似解1(最大誤差約5%)の順に,厳密解との差が大きくなっていることがわかります.
近似式の複雑性は,その逆順なので,複雑な近似式のほうが計算精度が高い,という結果になりました.
ただし,計算精度が相対的に低い近似式1でも約5%しかずれていないので,実用上は近似式1でも問題ないと考えます.
おまけ:\( f_{z} \le 2\sqrt{a_{p} (2R - a_{p}) } \le 2R \)の意味
近似解2と3が使える範囲を定めている数式なのですが,これは端的に言えばノーズRだけで加工面が生成されていることを担保するための数式です.
下記2式を組み合わせて作られていると推定します.
- \( f_{z} \le 2R \):1回転あたりの送り量\( f_{z} \)をがノーズR部分よりも大きくならないように制限
- \( f_{z} \le 2\sqrt{a_{p} (2R - a_{p}) } = 2\sqrt{ R^2 - (R - a_{p})^2 } \):ノーズRと切込み深さ\( a_{p} \)が決まると,ノーズRだけで加工面が生成されるための1回転あたりの送り量\( f_{z} \)の最大値が決まるので,それを制限